电力需求预测赛

题目

题目链接点这里 ## 赛题背景

随着全球经济的快速发展和城市化进程的加速，电力系统面临着越来越大的挑战。电力需求的准确预测对于电网的稳定运行、能源的有效管理以及可再生能源的整合至关重要。

然而，电力需求受到多种因素的影响，为了提高电力需求预测的准确性和可靠性，推动智能电网和可持续能源系统的发展，本场以“电力需求预测”为赛题的数据算法挑战赛。选手需要根据历史数据构建有效的模型，能够准确的预测未来电力需求。

赛题任务

给定多个房屋对应电力消耗历史N天的相关序列数据等信息，预测房屋对应电力的消耗。

评审规则

数据说明

赛题数据由训练集和测试集组成，为了保证比赛的公平性，将每日日期进行脱敏，用1-N进行标识，即1为数据集最近一天，其中1-10为测试集数据。数据集由字段id（房屋id）、 dt（日标识）、type（房屋类型）、target（实际电力消耗）组成。

\[ \begin{array}{|l|l|} \hline \text { 特征字段 } & \text { 字段描述 } \\ \hline \text { id } & \text { 房屋id } \\ \hline \text { dt } & \text { 日标识 } \\ \hline \text { type } & \text { 房屋类型 } \\ \hline \text { target } & \text { 实际电力消耗，预测目标 } \\ \hline \end{array} \]

评审规则

预测结果以 MES(Mean Square Error) 作为评判标准，具体公式如下： \[ \frac{1}{n} \sum_{n=1}^n\left(y_i-\bar{y}_i\right)^2 \] 其中，\(y_i\) 是真实电力消耗，\(\bar{y}_i\) 是预测电力消耗。

数据下载

文件名	下载
电力需求预测挑战赛数据集.zip	下载文件
电力需求预测挑战赛提交示例.csv	下载文件

Task 1

baseline 的代码如下：

# 1. 导入需要用到的相关库
# 导入 pandas 库，用于数据处理和分析
import pandas as pd
# 导入 numpy 库，用于科学计算和多维数组操作
import numpy as np

# 2. 读取训练集和测试集
# 使用 read_csv() 函数从文件中读取训练集数据，文件名为 'train.csv'
train = pd.read_csv('../dataset/train.csv')
# 使用 read_csv() 函数从文件中读取测试集数据，文件名为 'train.csv'
test = pd.read_csv('../dataset/test.csv')

# 3. 计算训练数据最近11-20单位时间内对应id的目标均值
target_mean = train[train['dt']<=20].groupby(['id'])['target'].mean().reset_index()

# 4. 将target_mean作为测试集结果进行合并
test = test.merge(target_mean, on=['id'], how='left')

# 5. 保存结果文件到本地
test[['id','dt','target']].to_csv('submit.csv', index=None)

将 baseline 的结果提交后可得 MSE 得分为：373.89846

接下来我们来分析一下 baseline 代码：

可以看到 baseline 主要通过了如下几个步骤对数据进行处理：

1. 导入库：首先，代码导入了需要用到的库，包括 pandas（用于数据处理和分析）。
2. 读取数据：代码通过使用 pd.read_csv 函数从文件中读取训练集和测试集数据，并将其存储在 train.csv 和 test.csv 两个数据框中。
3. 计算最近时间的用电均值：
   • 计算训练数据最近11-20单位时间内对应id的目标均值，可以用来反映最近的用电情况。
4. 将用电均值直接作为预测结果：
   • 这里使用merge函数根据'id'列将test和target_mean两个DataFrame进行左连接，这意味着测试集的所有行都会保留。
5. 保存结果文件到本地：
   • 使用to_csv()函数将测试集的'id'、'dt'和'target'列保存为CSV文件，文件名为'submit.csv'。index=None参数表示在保存时不包含行索引。

我们可以看到，上述代码中的选取的是训练数据最近11-20单位时间内对应id的目标均值，那么如果我们选取所有数据再取平均值呢？

train = pd.read_csv('../dataset/train.csv')
test = pd.read_csv('../dataset/test.csv')

# 计算训练数据最近11-506单位时间内对应id的目标均值
target_mean = train[train['dt']<=506].groupby(['id'])['target'].mean().reset_index()

# 将target_mean作为测试集结果进行合并
test = test.merge(target_mean, on=['id'], how='left')

# 保存结果文件到本地
test[['id','dt','target']].to_csv('submit.csv', index=None)

将结果提交后可得 MSE 得分为：629.76628

效果更差了，这是因为这是一个时序预测的题目，当选取所有数据进行预测时，就会导致效果较差，应当选取待预测附近的一些数据进行预测。

Task 2

基础概念

1. GBDT

   GBDT (Gradient Boosting Decision Tree) 是机器学习中一个长盛不衰的模型，其主要思想是利用弱分类器（决策树）迭代训练以得到最优模型，该模型具有训练效果好、不易过拟合等优点。

2. LightGBM

   LightGBM（Light Gradient Boosting Machine）是一个实现GBDT算法的框架，支持高效率的并行训练，并且具有更快的训练速度、更低的内存消耗、更好的准确率、支持分布式可以快速处理海量数据等优点。

在 Task 2 中，我们将使用 LightGBM 模型。

LightGBM

我们先来看代码：

导入模块

import numpy as np
import pandas as pd
import lightgbm as lgb
from sklearn.metrics import mean_squared_log_error, mean_absolute_error, mean_squared_error
import tqdm
import sys
import os
import gc
import argparse
import warnings
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
import seaborn as sns
warnings.filterwarnings('ignore')

plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置字体为黑体
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题

导入必要的库，包括 numpy、pandas、lightgbm、sklearn 和 matplotlib 等。

设置中文字体，避免出现乱码问题。

设置忽略警告信息，以便代码运行时不显示警告。

读取数据

读取训练数据和测试数据，并存储在 train 和 test 中。

train = pd.read_csv('../dataset/train.csv')
test = pd.read_csv('../dataset/test.csv')
print('****************train*****************')
print(train)
print('\n*************test*************')
print(test)

****************train*****************
                 id   dt  type  target
0        00037f39cf   11     2  44.050
1        00037f39cf   12     2  50.672
2        00037f39cf   13     2  39.042
3        00037f39cf   14     2  35.900
4        00037f39cf   15     2  53.888
...             ...  ...   ...     ...
2877300  fff81139a7  502     5  28.552
2877301  fff81139a7  503     5  22.818
2877302  fff81139a7  504     5  21.282
2877303  fff81139a7  505     5  22.021
2877304  fff81139a7  506     5  18.145

[2877305 rows x 4 columns]

*************test*************
               id  dt  type
0      00037f39cf   1     2
1      00037f39cf   2     2
2      00037f39cf   3     2
3      00037f39cf   4     2
4      00037f39cf   5     2
...           ...  ..   ...
58315  fff81139a7   6     5
58316  fff81139a7   7     5
58317  fff81139a7   8     5
58318  fff81139a7   9     5
58319  fff81139a7  10     5

[58320 rows x 3 columns]

数据可视化

柱状图

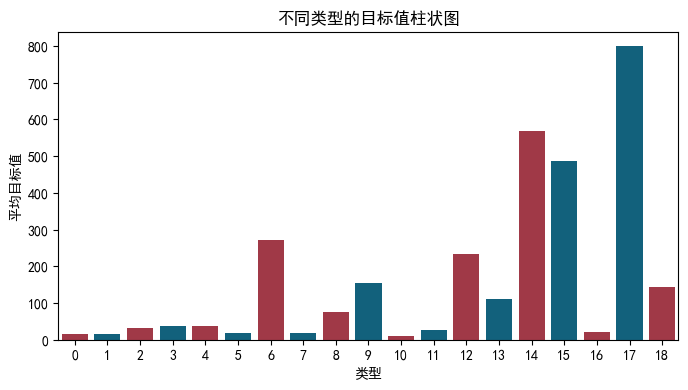
不同 type 类型对应 target 的柱状图：

type_target_df = train.groupby('type')['target'].mean().reset_index()

# 使用Seaborn绘制柱状图
plt.figure(figsize=(8, 4))
sns.barplot(x='type', y='target', data=type_target_df, palette=["#b1283a", "#006a8e"])
plt.xlabel('类型')
plt.ylabel('平均目标值')
plt.title('不同类型的目标值柱状图')
plt.show()

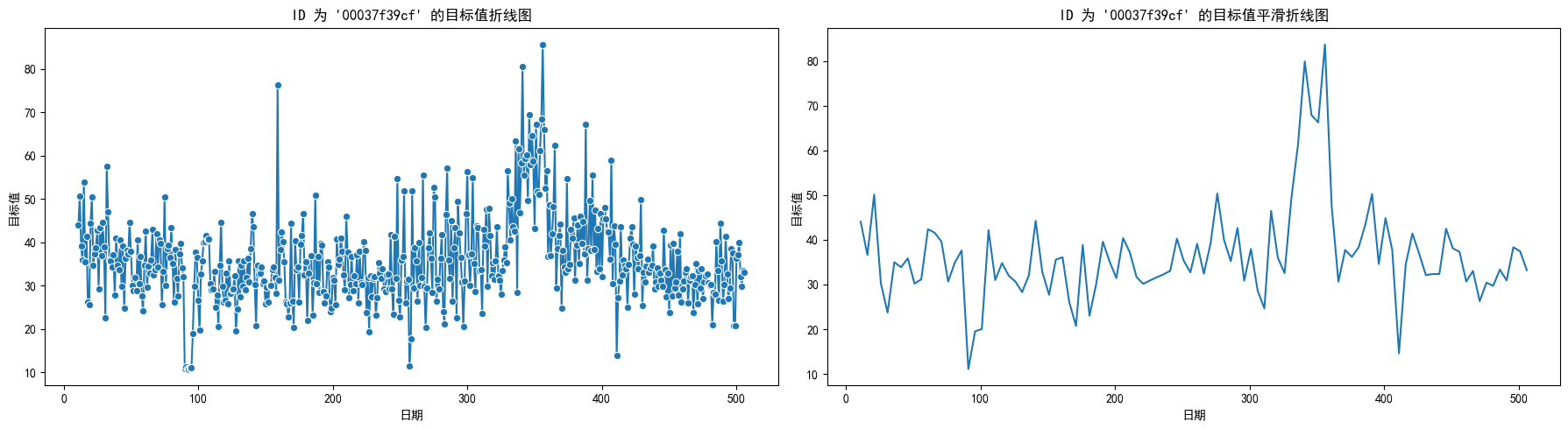
折线图

id 为 00037f39cf 的按dt为序列关于 target 的折线图：

并且由于数据较多，原始折线图并不美观且为了直观的看出 target 的变化趋势，我们对其进行了平滑处理。

UnivariateSpline 是 scipy 库中用于一元函数插值和平滑的工具。其基本思想是通过一个平滑函数来逼近数据点，使得曲线更加平滑，同时尽可能贴合原始数据。

数学原理：

好的，让我们详细解释一下使用 UnivariateSpline 进行平滑处理的原理以及代码中各个参数的作用和计算过程。

平滑处理的原理

UnivariateSpline 是 scipy 库中用于一元函数插值和平滑的工具。

其基本思想是通过一个平滑函数来逼近数据点，使得曲线更加平滑，同时尽可能贴合原始数据。

数学原理

假设我们有一组数据点 \((x_i, y_i)\)，希望找到一个平滑函数 \(s(x)\) 来逼近这些数据点。

UnivariateSpline 使用最小二乘法来找到一个平滑的三次样条函数（cubic spline），即最小化以下目标函数：

\[ \sum_{i=1}^{n} \left( y_i - s(x_i) \right)^2 + \lambda \int_{a}^{b} \left( s''(x) \right)^2 dx \]

其中： - \(\left( y_i - s(x_i) \right)^2\) 是数据点与平滑曲线之间的误差。 - \(\int_{a}^{b} \left( s''(x) \right)^2 dx\) 是平滑曲线的二阶导数的积分，用于控制曲线的平滑程度。 - \(\lambda\) 是平滑参数，控制拟合的平滑程度。较大的 \(\lambda\) 值会产生更平滑的曲线，但可能会偏离数据点；较小的 \(\lambda\) 值会产生更贴合数据点的曲线，但可能会有较大的波动。

# 筛选特定 id 的数据
specific_id_df = train[train['id'] == '00037f39cf']

# 创建子图
fig, axes = plt.subplots(1, 2, figsize=(18, 5))

# 子图1：原始折线图
sns.lineplot(ax=axes[0], x='dt', y='target', data=specific_id_df, marker='o')
axes[0].set_xlabel('日期')
axes[0].set_ylabel('目标值')
axes[0].set_title("ID 为 '00037f39cf' 的目标值折线图")

# 子图2：平滑后的折线图
# 准备数据
x = specific_id_df['dt']
y = specific_id_df['target']

# 使用UnivariateSpline进行平滑处理
spl = UnivariateSpline(x, y)
xs = np.linspace(x.min(), x.max(), 100)
ys = spl(xs)

# 绘制平滑后的折线图
sns.lineplot(ax=axes[1], x=xs, y=ys)
axes[1].set_xlabel('日期')
axes[1].set_ylabel('目标值')
axes[1].set_title("ID 为 '00037f39cf' 的目标值平滑折线图")

# 调整布局
plt.tight_layout()
plt.show()

部分代码解释：

• UnivariateSpline(x, y)：创建一个三次样条插值对象，自动选择平滑参数 \(\lambda\)。
• np.linspace(x.min(), x.max(), 100)：在 x 的范围内生成 100 个均匀分布的点，用于绘制平滑曲线。
• spl(xs)：使用三次样条插值对象对新的自变量 xs 进行插值，得到平滑曲线的因变量 ys。

数据预处理

合并和排序数据

合并训练数据和测试数据，并按 id 和 dt 排序。

data = pd.concat([test, train], axis=0, ignore_index=True)
data = data.sort_values(['id','dt'], ascending=False).reset_index(drop=True)
print(data)

                 id   dt  type  target
0        fff81139a7  506     5  18.145
1        fff81139a7  505     5  22.021
2        fff81139a7  504     5  21.282
3        fff81139a7  503     5  22.818
4        fff81139a7  502     5  28.552
...             ...  ...   ...     ...
2935620  00037f39cf    5     2     NaN
2935621  00037f39cf    4     2     NaN
2935622  00037f39cf    3     2     NaN
2935623  00037f39cf    2     2     NaN
2935624  00037f39cf    1     2     NaN

[2935625 rows x 4 columns]

历史平移

时间序列数据具有趋势和季节性模式。历史平移特征可以帮助模型识别这些模式。

在本题中即电力需求可能具有每日、每周或每月的周期性变化。

并且一般具有时间依赖性，即当前值可能依赖于过去的值。通过引入历史平移特征，模型能够捕捉这种时间依赖性，从而提高预测性能。

进行历史平移（lagging）是时间序列数据处理中一种常见的特征工程方法，特别是在预测任务中。

其主要目的是通过引入过去一段时间的目标值作为特征，帮助模型更好地理解和预测未来的趋势和模式。

假设我们有一个时间序列数据集 \(\{y_t\}\)，其中 \(y_t\) 是时间 \(t\) 的目标值。为了预测未来的目标值 \(y_{t+k}\)（这里 \(k\) 是预测的步长），我们可以引入过去的目标值作为特征。

对于每个时间 \(t\)，生成的历史平移特征可以表示为：

\[ \text{lag}_k(y_t) = y_{t-k} \]

其中，\(\text{lag}_k(y_t)\) 表示第 \(k\) 个滞后的目标值。

例如，对于时间 \(t\) 的目标值 \(y_t\)，引入前 10 到 30 天的历史平移特征可以表示为：

\[ \{ y_{t-10}, y_{t-11}, \ldots, y_{t-30} \} \]

下面对每个 id 进行分组，并生成前 10 到 30 天的 target 平移特征。

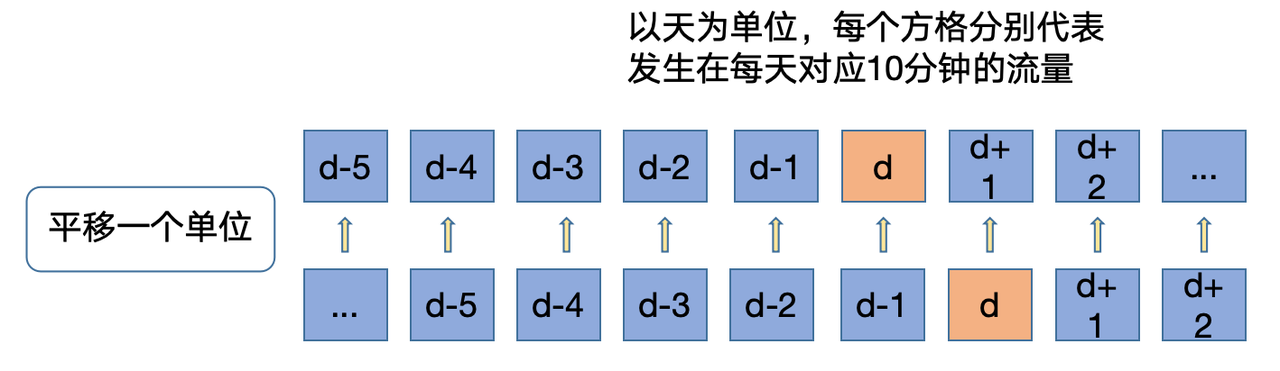
for i in range(10,30):
    data[f'last{i}_target'] = data.groupby(['id'])['target'].shift(i)

• 使用 groupby(['id']) 对每个 id 进行分组，以处理不同房屋的时间序列数据。
• 使用 shift(i) 生成前 i 天的 target 平移特征。shift(i) 函数会将目标值向下移动 i 个位置，从而生成相应的历史特征。
• 生成的特征命名为 last{i}_target，例如 last10_target 表示前第 10 天的 target 值。

窗口统计

生成窗口统计特征是一种常见的特征工程方法，特别适用于时间序列数据。这些特征可以帮助模型捕捉时间序列数据中的短期趋势和变化，从而提高预测性能。

计算前 10 到 12 天的 target 均值，生成窗口统计特征。

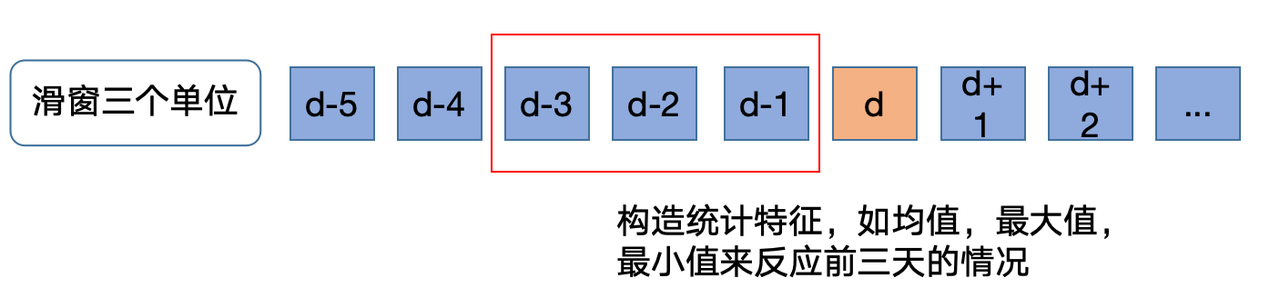
data[f'win3_mean_target'] = (data['last10_target'] + data['last11_target'] + data['last12_target']) / 3

数据分割

根据 target 是否为空，将数据重新划分为训练集和测试集。

train = data[data.target.notnull()].reset_index(drop=True)
test = data[data.target.isnull()].reset_index(drop=True)

确定输入特征

1. 排除 id 列

   • 无预测价值：

     id 是房屋的标识，它不包含任何关于目标变量的信息，不具有实际的预测价值。

2. 排除 target 列

   • 防止数据泄漏：

     target 列是我们要预测的目标变量。如果在模型训练过程中将 target 作为输入特征，会导致数据泄漏，模型直接学习目标值，而不是数据中的实际模式和关系。

train_cols = [f for f in data.columns if f not in ['id','target']]

定义模型训练函数

代码

def time_model(lgb, train_df, test_df, cols):
    # 训练集和验证集切分
    trn_x, trn_y = train_df[train_df.dt>=31][cols], train_df[train_df.dt>=31]['target']
    val_x, val_y = train_df[train_df.dt<=30][cols], train_df[train_df.dt<=30]['target']
    # 构建模型输入数据
    train_matrix = lgb.Dataset(trn_x, label=trn_y)
    valid_matrix = lgb.Dataset(val_x, label=val_y)
    # lightgbm参数
    lgb_params = {
        'boosting_type': 'gbdt',
        'objective': 'regression',
        'metric': 'mse',
        'min_child_weight': 5,
        'num_leaves': 2 ** 5,
        'lambda_l2': 10,
        'feature_fraction': 0.8,
        'bagging_fraction': 0.8,
        'bagging_freq': 4,
        'learning_rate': 0.05,
        'seed': 666,
        'nthread' : 16,
        'verbose' : -1,
        'early_stopping_rounds': 500,
        'verbose_eval':500
    }
    # 训练模型
    model = lgb.train(lgb_params, train_matrix, 50000, valid_sets=[valid_matrix],
                      categorical_feature=[])
    # 验证集和测试集结果预测
    val_pred = model.predict(val_x, num_iteration=model.best_iteration)
    test_pred = model.predict(test_df[cols], num_iteration=model.best_iteration)
    # 离线分数评估
    score = mean_squared_error(val_pred, val_y)
    print(score)
       
    return val_pred, test_pred

在上述代码中：

• 切分训练集和验证集。dt 大于等于 31 作为训练集，小于等于 30 作为验证集。
• 创建 LightGBM 数据矩阵。
• 定义 LightGBM 参数，包括：

\[ \begin{array}{|c|c|} \hline \text { 参数 } & \text { 值 } \\ \hline \text { boosting\_type (提升方法) } & \text { gbdt } \\ \hline \text { objective (目标函数) } & \text { regression } \\ \hline \text { metric (评估指标) } & \text { mse } \\ \hline \text { min\_child\_weight (叶子节点最小权重) } & 5 \\ \hline \text { num\_leaves (叶子节点数) } & 32 \\ \hline \text { lambda\_12 (L2 正则化系数) } & 10 \\ \hline \text { feature\_fraction (特征采样率) } & 0.8 \\ \hline \text { bagging\_fraction (样本采样率) } & 0.8 \\ \hline \text { bagging\_freq (采样频率) } & 4 \\ \hline \text { learning\_rate (学习率) } & 0.05 \\ \hline \text { seed (随机种子) } & 2024 \\ \hline \text { nthread (线程数) } & 16 \\ \hline \text { verbose (输出信息级别) } & -1 \\ \hline \end{array} \]

• 训练模型，并在验证集上进行预测和评估。

---

参数详解：

• boosting_type
  • 含义：指定提升（boosting）的类型。这里使用的是GBDT。

GBDT详解

GBDT 即 Gradient Boosting Decision Tree（梯度提升决策树），是一种集成学习方法。它通过构建多个决策树并逐步改进模型的预测能力来提升整体性能。

---

工作原理

GBDT 通过逐步添加决策树，每一步的新树都是在前一步模型的残差上进行训练的。其核心思想是使用梯度下降法来最小化损失函数。

下面我们来详细地看看 GBDT 的工作原理：

1. 初始化模型
   初始化模型 \(F_0(x)\) 是选择一个常数值 \(\gamma\) ，使得损失函数 \(L\) 的和最小化。 \[ F_0(x) = \arg\min_{\gamma} \sum_{i=1}^n L(y_i, \gamma) \] 其中：

   • $ L $ 是损失函数

   • $ y_i $ 是实际值

   • $ $ ：

     • 含义：\(\gamma\) 是初始模型的预测值，它是一个常数。

       在训练开始时，模型 \(F_0(x)\) 对所有输入 \(x\) 都输出这个常数值 \(\gamma\) 。

     • 来源：\(\gamma\) 的值是通过最小化初始损失函数来确定的。

       具体来说， \(\gamma\) 是使损失函数 \(\sum_{i=1}^n L\left(y_i, \gamma\right)\) 最小化的常数。

2. 计算残差
   对于每个样本，计算当前模型的残差（也称为负梯度），即目标值和当前模型预测值之间的差异。 \[ r_{i,m} = -\left[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right]_{F=F_{m-1}} \] 在平方误差情况下，残差可以简化为： \[ r_{i,m} = y_i - F_{m-1}(x_i) \]

3. 拟合新树
   用残差作为目标值，训练一个新的决策树 $ h_m(x) \(。\)$ h_m(x) = {h} {i=1}^n (r_{im} - h(x_i))^2 $$

4. 更新模型
   将新的决策树加入到模型中，更新后的模型为： \[ F_m(x) = F_{m-1}(x) + \gamma_m h_m(x) \] 其中，$ _m $ 是学习率，控制新树对模型的贡献大小。

5. 重复步骤 2 到 4
   重复上述步骤，直到达到预定的迭代次数或误差满足要求。

---

损失函数

GBDT 的目标是最小化损失函数 $ L $，常见的损失函数包括：

• 均方误差（MSE）

\[ L(y, \hat{y}) = \frac{1}{2} (y - \hat{y})^2 \]

• 交叉熵损失（分类问题）

\[ L(y, \hat{y}) = -[y \log(\hat{y}) + (1 - y) \log(1 - \hat{y})] \]

---

梯度下降

在每次迭代中，GBDT 使用梯度下降法来优化模型。对于给定的损失函数 $ L $，梯度的计算方式为：

\[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \]

这个梯度表示了当前模型的预测与实际值之间的差异。在平方误差情况下，梯度（残差）为：

\[ r_{i,m} = y_i - F_{m-1}(x_i) \]

---

新树的训练

新的决策树 $ h_m(x) $ 是通过最小化残差的平方和来训练的，即： \[ h_m(x) = \arg\min_{h} \sum_{i=1}^n (r_{i,m} - h(x_i))^2 \]

---

• objective

  • 含义：定义模型的目标函数。这里使用的是回归（regression）。

  • 数学原理：目标函数是均方误差（MSE），即：

    \[ \text{MSE} = \frac{1}{n} \sum_{i=1}^n (\hat{y}_i - y_i)^2 \]

• metric

  • 含义：评估模型性能的指标。这里使用的是均方误差（MSE）。
  • 数学原理：评估模型预测值与实际值之间的差异，均方误差的公式如上。

• min_child_weight

  • 含义：一个叶子节点中最小的样本权重和。
  • 数学原理：控制叶子节点的最小 Hessian 和（即二阶导数和），避免叶子节点样本数过少，防止过拟合。

• num_leaves

  • 含义：树的最大叶子数。这里设置为 32。

  • 数学原理：叶子数越多，树的复杂度越高，可以捕捉更多的细节，但也可能导致过拟合。叶子数与树的深度 \(d\) 关系为：

    \[ \text{num\_leaves} = 2^d \]

• lambda_l2

  • 含义：L2 正则化系数（也叫 reg_lambda）。

  • 数学原理：增加权重的平方和惩罚项，防止过拟合。正则化项为：

    \[ \Omega(f) = \gamma T + \frac{1}{2} \lambda \|w\|^2 \]

    其中，\(\lambda\) 为 lambda_l2。

• feature_fraction

  • 含义：在每次迭代中随机选择的特征比例。这里设置为 0.8。
  • 数学原理：每棵树只使用部分特征进行训练，减少过拟合，提高模型的泛化能力。

• bagging_fraction

  • 含义：在每次迭代中随机选择的样本比例。这里设置为 0.8。
  • 数学原理：每次迭代使用部分数据样本进行训练，类似于 Bagging 方法，减少过拟合。

• bagging_freq

  • 含义：执行 bagging 的频率。这里设置为 4。
  • 数学原理：每 4 次迭代进行一次样本的重采样。

• learning_rate

  • 含义：学习率，控制每棵树对模型的贡献大小。这里设置为 0.05。

  • 数学原理：较小的学习率可以让模型更平滑地逼近目标函数，但需要更多的树来收敛。更新模型的公式为：

    \[ F_m(x) = F_{m-1}(x) + \gamma h_m(x) \]

    其中，\(\gamma\) 是学习率。

• seed

  随机种子，用于重现结果。这里设置为 2024。

  设置随机种子可以确保每次运行结果一致，便于我们进行调试和验证模型效果。

• nthread

  线程数量，控制并行计算的线程数。这里设置为 16，多线程可以加速训练过程。

• verbose

  控制训练过程的输出信息。设置为 -1 表示不输出详细信息，减少日志信息的输出，提高训练过程的简洁性。

LightGBM

在看完了上述的代码后及其参数后，我们来看一下 LightGBM 的具体原理。

LightGBM 是一种高效的梯度提升决策树实现，旨在提高 GBDT 的训练速度和预测精度。

LightGBM 的关键特性和数学原理：

1. 基于叶子节点的增长策略（Leaf-wise Growth）
2. 基于直方图的算法（Histogram-based Algorithm）
3. 梯度单边采样（Gradient-based One-Side Sampling, GOSS）
4. 特征并行和数据并行（Feature and Data Parallelism）

基于叶子节点的增长策略（Leaf-wise Growth）

LightGBM 使用 leaf-wise（基于叶子节点的增长策略）而不是 level-wise（基于层的增长策略），每次选择具有最大增益的叶子节点进行分裂。

• 增益计算：

  \[ \text{Gain} = \frac{1}{2} \left( \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} \right) - \gamma \]

  其中：

  • $ G_L $ 和 $ G_R $ 分别是左、右子节点的梯度和
  • $ H_L $ 和 $ H_R $ 分别是左、右子节点的二阶梯度和
  • \(\lambda\) 是 L2 正则化参数
  • \(\gamma\) 是叶子节点分裂的惩罚项
  • 左子节点梯度和: \(G_L=\sum_{x_i \leq \text { split }} g_i\)
  • 右子节点梯度和： \(G_R=\sum_{x_i>\text { split }} g_i\)
  • 左子节点二阶梯度和: \(H_L=\sum_{x_i \leq \text { split }} h_i\)
  • 右子节点二阶梯度和: \(H_R=\sum_{x_i>\text { split }} h_i\)

---

基于直方图的算法（Histogram-based Algorithm）

LightGBM 使用直方图算法将连续特征值离散化为有限数量的 bin，大大减少了计算量。每次分裂节点时，LightGBM 会计算所有特征的直方图，然后选择最佳分裂点。

• 直方图构建以及直方图加速分裂原理：

  1. 离散化特征值：

     将连续特征值划分为 \(k\) 个 bin，每个 bin 表示一个区间。

     • 离散化 (分箱)：将连续特征值 \(x_i\) 转换为离散的 bin 索引 \(b_j\) 。
     • 公式: 假设特征值 \(X\) 的范围是 \([a, b]\) ，划分为 \(k\) 个 bin，每个 bin 的宽度为 \(\Delta=\frac{b-a}{k}\) \[ \operatorname{bin}_j=[a+(j-1) \Delta, a+j \Delta) \]
     • 分配样本到 bin: 对于每个样本 \(x_i\) ，确定其所属的 bin 索引 \(j\) : \[ j=\left\lfloor\frac{x_i-a}{\Delta}\right\rfloor \]

  2. 统计每个 bin 中的样本数量和梯度：

     对于每个 $ bin_j $ ，计算其包含的样本数量 \(N_j\) 、样本的一阶梯度和 \(G_j\) 以及二阶梯度和 \(H_j\) 。

     • 样本数量统计： \[ N_j = \sum_{i=1}^{n} \mathbb{I}(x_i \in \text{bin}_j) \] 其中，

       • $ N_j $ 表示 $ bin_j $ 中样本的数量

       • \(\mathbb{I}\) 是指示函数，表示样本 $ x_i $ 是否属于 $ bin_j $。即： \[ \mathbb{I}\left(x_i \in \operatorname{bin}_j\right)= \begin{cases}1, & \text { 如果 } x_i \in \operatorname{bin}_j \\ 0, & \text { 如果 } x_i \notin \operatorname{bin}_j\end{cases} \]

     • 梯度和统计： \[ \begin{aligned}G_j & =\sum_{i=1}^n \mathbb{I}\left(x_i \in \operatorname{bin}_j\right) g_i \\H_j & =\sum_{i=1}^n \mathbb{I}\left(x_i \in \operatorname{bin}_j\right) h_i\end{aligned} \] 其中，

       • \(G_j\) 表示 $ bin_j $ 的一阶梯度和，\(g_i\) 是样本 \(x_i\) 的一阶梯度
       • \(H_j\) 表示 $ bin_j $ 的二阶梯度和，\(h_i\) 是样本 \(x_i\) 的二阶梯度

  3. 计算每个分裂点的增益
     在计算增益时，我们需要遍历所有可能的分裂点，计算每个分裂点的增益。

  4. 遍历所有可能的分裂点，计算增益
     我们需要遍历所有可能的分裂点，计算每个分裂点的增益，并选择增益最大的分裂点作为最佳分裂点。

     1. 初始化增益和最佳分裂点：
        best_gain \(=-\infty\)
        best_split \(=\) None

     2. 遍历所有分裂点：

        对于每个可能的分裂点，计算其增益，并更新最佳增益和最佳分裂点。 for each split point \(s_j\) : \[ \begin{aligned} for\ & each\ split\ point\ s_j:\\ & G_L =\sum_{x_i \leq s_j} g_i \\ & H_L =\sum_{x_i \leq s_j} h_i \\ & G_R =\sum_{x_i>s_j} g_i \\ & H_R =\sum_{x_i>s_j} h_i \end{aligned} \]

        计算增益并更新最佳增益和最佳分裂点： \[ \begin{aligned} if\ G & ain\_j\ >\ best\_gain\ :\\ & best\_gain\ =\ Gain_j\\ & best\_split\ =\ s_j \end{aligned} \]

  5. 选择最佳分裂点
     最终，选择具有最大增益的分裂点作为最佳分裂点。
     最佳分裂点 = best_split
     

  最佳增益 = best_gain

梯度单边采样（GOSS）

GOSS 通过保持大梯度的数据点，随机采样小梯度的数据点来减少计算量，同时保持模型的准确性。

• 大梯度样本保留：
  保留那些具有较大梯度的样本，因为这些样本对提升的损失函数贡献最大。

• 小梯度样本采样：
  随机采样那些具有较小梯度的样本，减少计算量，并通过对小梯度样本赋予更大的权重来平衡样本分布。

GOSS 的步骤

>GOSS 伪代码，引自Lightgbm基本原理介绍

假设我们有一个样本 \(\left\{\left(x_i, y_i\right)\right\}_{i=1}^n\) ，其梯度为 \(\left\{g_i\right\}_{i=1}^n\) 。

以下是 GOSS 的具体步骤:

1. 计算每个样本的梯度:

   • 对于每个样本 \(i\) ，计算其梯度 \(g_i\) : \[ g_i=\frac{\partial L\left(y_i, \hat{y}_i\right)}{\partial \hat{y}_i} \] 其中， \(L\) 是损失函数， \(y_i\) 是实际值， \(\hat{y}_i\) 是预测值。

2. 排序样本梯度:

   • 将样本按梯度的绝对值 \(\left|g_i\right|\) 从大到小排序。

3. 选择大梯度样本:

   • 选择前 \(a \cdot n\) 个梯度较大的样本，其中 \(a\) 是一个比例参数。

4. 随机采样小梯度样本:

   • 从剩余的 \((1-a) \cdot n\) 个样本中随机选择 \(b \cdot n\) 个梯度较小的样本，其中 \(b\) 也是一个比例参数。

5. 调整小梯度样本的权重:

   • 为了平衡样本分布，对小梯度样本的梯度进行放大，放大系数为 \(\frac{1-a}{b}\) 。

特征并行和数据并行

LightGBM 支持特征并行和数据并行，通过多线程和分布式计算进一步加速训练过程。

训练和预测并保存结果

使用 time_model 函数训练模型，并进行验证和测试集预测。

train_cv = train
test_cv = test
train_cols_cv = train_cols
lgb_oof, lgb_test = time_model(lgb, train, test, train_cols)

184.6440690468036

将测试集预测结果保存到 submit.csv 文件中。

test['target'] = lgb_test
test[['id','dt','target']].to_csv('submit.csv', index=None)

提交结果，可以看到得分为：259.9667

相对于 Task 1 有较大的提升。

超参数优化

import numpy as np
import pandas as pd
import lightgbm as lgb
from lightgbm import LGBMRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import GridSearchCV
import warnings
warnings.filterwarnings('ignore')

def time_model_gc(train_df, test_df, cols):
    # 训练集和验证集切分
    trn_x, trn_y = train_df[train_df.dt >= 31][cols], train_df[train_df.dt >= 31]['target']
    val_x, val_y = train_df[train_df.dt <= 30][cols], train_df[train_df.dt <= 30]['target']
    
    # 构建模型输入数据
    train_matrix = lgb.Dataset(trn_x, label=trn_y)
    valid_matrix = lgb.Dataset(val_x, label=val_y, reference=train_matrix)

    # 定义参数网格
    param_grid = {
        'learning_rate': [0.01, 0.05],
        'num_leaves': [16, 32],
        'max_depth': [5, 10, 20],
        'min_child_weight': [5, 10],
        'subsample': [0.8, 1.0],
        'reg_lambda': [0.1, 0.5],
        'colsample_bytree': [0.8, 1]
    }

    # 初始化LGBMRegressor，使用GPU
    lgb_model = LGBMRegressor(
        boosting_type='gbdt',
        objective='regression',
        metric='mse',
       # min_child_weight=5,
       # num_leaves=2 ** 5,
        reg_lambda=10,
       # colsample_bytree=0.8,
       # subsample=0.8,
        subsample_freq=4,
        learning_rate=0.05,
        seed=666,
        n_jobs=16,
        verbose=0,
        device='gpu',
        gpu_platform_id=0,
        gpu_device_id=0
    )

    # 进行网格搜索
    print("开始网格搜索...")
    grid_search = GridSearchCV(estimator=lgb_model, param_grid=param_grid, scoring='neg_mean_squared_error', cv=5, verbose=1)
    grid_search.fit(trn_x, trn_y)
    best_params = grid_search.best_params_
    print(f"最佳参数: {best_params}")
    print(f"最佳评分: {-grid_search.best_score_}")

    # 使用最佳参数重新训练模型
    print("开始重新训练模型...")
    lgb_model = lgb.train(
        params=best_params,
        train_set=train_matrix,
        valid_sets=[train_matrix, valid_matrix],
        num_boost_round=5000,
        early_stopping_rounds=500,
        verbose_eval=200
    )

    # 验证集预测
    print("开始验证集预测...")
    val_pred = lgb_model.predict(val_x, num_iteration=lgb_model.best_iteration)
    mse = mean_squared_error(val_y, val_pred)
    print(f'Validation Mean Squared Error: {mse}')

    # 测试集预测
    print("开始测试集预测...")
    test_pred = lgb_model.predict(test_df[cols], num_iteration=lgb_model.best_iteration)

    return val_pred, test_pred, val_x.index

train = train_cv
test = test_cv
train_cols = train_cols_cv

# 调用 time_model_gc 函数并接收结果
val_pred, test_pred, val_index= time_model_gc(train, test, train_cols)

开始网格搜索...
Fitting 5 folds for each of 1296 candidates, totalling 6480 fits

# 保存验证集预测结果
val_results = pd.DataFrame({
    'id': train['id'][train['dt'] <= 30],
    'dt': train['dt'][train['dt'] <= 30],
    'actual': train['target'][train['dt'] <= 30],
    'predicted': val_pred
})

# 保存验证集预测结果
val_results = pd.DataFrame({
    'id': train.loc[val_index, 'id'],
    'dt': train.loc[val_index, 'dt'],
    'type': train.loc[val_index, 'type'],
    'target': val_pred
}

val_results.to_csv('validation_predictions.csv', index=False)

# 保存测试集预测结果
test_results = pd.DataFrame({
    'id': test['id'],
    'dt': test['dt'],
    'type': test['type'],
    'target': test_pred
})

test_results.to_csv('test_predictions.csv', index=False)