概率论习题(2)

t15

设随机变量 X 的分布函数为 \[ F(x)=\left\{\begin{array}{c} 0, & x<0, \\ \frac{1}{2}, & 0 \leq x<1, \\ 1-e^{-x}, & x \geq 1, \end{array}\right. \]

求 $P\{X=1\}$

解析

根据事件概率与分布函数极限的关系有 \[ P\{X=1\}=\lim _{x \rightarrow 1^{+}} F(x)-\lim _{x \rightarrow 1^{-}} F(x)=1-e^{-1}-\frac{1}{2}=\frac{1}{2}-e^{-1} \]

随机变量的分布，《知识点总结》的 $\S 2.1$

t16

设随机变量 $X$ 的分布函数为 \[ F(x)=\left\{\begin{array}{ll} 0, & x<0, \\ 1 / 4, & 0 \leqslant x<1 \\ 1 / 3, & 1 \leqslant x<3 \\ 1 / 2, & 3 \leqslant x<6, \\ 1, & x \geqslant 6 . \end{array}\right. \text {, } \]

试求 $X$ 的概率分布列及 $P(X<3), P(X \leqslant 3), P(X>1), P(X \geqslant 1)$.

解析

大致想象一下 $F(x)$ 的图像为阶梯状，这对应离散随机变量的分布函数形状，所以可以写出 $X$ 的分布列：

$X$ 的概率分布列为 \[ \begin{array}{c|cccc} \hline X & 0 & 1 & 3 & 6 \\ \hline P & \dfrac{1}{4} & \dfrac{1}{12} & \dfrac{1}{6} & \dfrac{1}{2} \\ \hline \end{array} \] 可以看到在 $F(x)$ 中分段点的值为 $X$ 的取值。 \[ \begin{array}{ll} P(X<3)=P(X=0)+P(X=1)=\dfrac{1}{3}, & P(X \leqslant 3)=1-P(X=6)=\dfrac{1}{2}, \\ P(X>1)=P(X=3)+P(X=6)=\dfrac{2}{3}, & P(X \geqslant 1)=1-P(X=0)=\dfrac{3}{4} . \end{array} \]

随机变量的分布，《知识点总结》的 $\S 2.1$

t17

设随机变量 $X$ 的概率密度为 $f(x)=\left\{\begin{array}{c}1-C|x|,-1<x<1 \\ 0, \text { 其他 }\end{array}\right.$

（1）求 $C$ 的值；

（2）求 $Y=X^2+1$ 的概率密度。

解析

（1）利用密度函数的正则性： \[ 1=\int_{-\infty}^{\infty}f(x)dx=\int_{-1}^{1}\left[1-C|x|\right]dx=2\int_{0}^{1}\left(1-Cx\right)dx=2-C \]

\[ \Rightarrow C=1 \]

（2）由于 \[ \begin{aligned} & F_Y(y)=P_Y\{Y \leqslant y\}=P_X\left\{X^2+1 \leqslant y\right\}=P_X\left\{X^2 \leqslant y-1\right\} \\ & =\left\{\begin{array}{cc} 0, & y<1 \\ P\{-\sqrt{y-1} \leqslant X \leqslant \sqrt{y-1}\}, & 1 \leqslant y<2 \\ 1, & y \geqslant 2 \end{array}\right. \\ & \end{aligned} \]

故当 $1 \leqslant y<2$ 时, 有 \[ F_Y(y)=\int_{-\sqrt{y-1}}^{\sqrt{y-1}}(1-|x|) \mathrm{d} x=2 \int_0^{\sqrt{y-1}}(1-x) \mathrm{d} x=1-(1-\sqrt{y-1})^2 \] $Y$ 的分布函数为 \[ F_y(y)=\left\{\begin{array}{cc} 0, & y<1 \\ 1-(1-\sqrt{y-1})^2, & 1 \leqslant y<2 \\ 1, & y \geqslant 2 \end{array}\right. \] $Y$ 的密度函数为 \[ f_Y(y)=\left\{\begin{array}{cc} \frac{1}{\sqrt{y-1}}-1, & 1<y<2 \\ 0, & \text { 其他 } \end{array}\right. \] $ps:$ 一个检查 $Y$ 密度函数正确性的技巧，$Y$ 的密度函数不为 $0$ 的区间，一定是 $X$ 不为 $0$ 的区间通过变换得到的。比如 $t17$ ，$X$ 的密度函数不为 $0$ 的区间为 $(-1,1)$ ，则 $X^2+1$ 后变为 $(1,2)$ ，即 $Y$ 密度函数不为 $0$ 的区间。

随机变量的分布，分布函数与概率密度函数，随机变量函数的分布《知识点总结》的 $\S 2.1 、2.6$

## t18

设随机变量 $X$ 的期望存在，概率密度 $p(x)$ 关于 $x=\mu$ 对称： $p(\mu+x)=p(\mu-x)$ ，证明： $E(x)=\mu$.

解析

\[ \begin{array}{ll} E(X)&=\displaystyle\int_{-\infty}^{\infty} x p(x) d x=\int_{-\infty}^{\infty} \mu p(x) d x+\int_{-\infty}^{\infty}(x-\mu) p(x) d x \quad(第一项积值为 \mu ，是对照结果凑出来的\mu) \\ &=\displaystyle\mu \int_{-\infty}^{\infty} p(x) d x+\int_{-\infty}^{\infty}(x-\mu) p(x) d x=\mu+\int_{-\infty}^{\infty}(x-\mu) p(x) d x \quad\text { (第二项考虑对称消去) }\\ &= \mu+\displaystyle\int_{-\infty}^{+\infty} t p(t+\mu) dt \quad \text{(令$t=x-\mu$)}\\ &= \mu \\ \end{array} \]

$\quad \text { 记 } f(t) =t p(t+\mu) \quad f(-t)=-t p(\mu-t)=-t p(t+\mu) \Rightarrow f(t)+f(-t)=0 \quad f(t) \text { 为奇函数，所以后一项积分值为0}$

t19

国际市场上对我国某种出口商品的每年需求量是个随机变量 $X$ (吨). $X$ 服从区间 $[300,500]$ 上的均匀分布.每销售出一吨商品, 可为国家赚取外汇1.5千元; 若销售不出, 则每吨商品需贮存费 0.5 千元. 求: 应组织多少货源,才能使平均收益最大?

解析

设组织该货源 $a$ 吨. 则显然应该有 $300 \leqslant a \leqslant 500$. 又记 $Y$ 为在 $a$ 吨货源的条件下的收益额 (单位:千元), 则收益额 $Y$ 为需求量 $X$ 的函数, 即 $Y=g(X)$. 由题设条件知: 当 $X \geqslant a$ 时, 则此 $a$ 吨货源全部售出, 共获利 $1.5 a$. 当 $X<a$ 时, 则售出 $X$ 吨 (获利 $1.5 X$ ), 且还有 $a-X$ 吨积压 (获利 $-0.5(a-X)$ ), 所以共获利 $1.5 X-0.5(a-X)$,由此知 \[ g(X)=\left\{\begin{array}{ll} 1.5 a, & \text { 若 } X \geqslant a, \\ 1.5 X-0.5(a-X), & \text { 若 } X<a \end{array}= \begin{cases}1.5 a, & \text { 若 } X \geqslant a, \\ 2 X-0.5 a, & \text { 若 } X<a .\end{cases}\right. \]

\[ \begin{aligned} E(Y)&=\int_{-\infty}^{\infty} g(x) p_X(x) \mathrm{d} x=\int_{300}^{500} g(x) \frac{1}{200} \mathrm{~d} x\\ & =\frac{1}{200}\left(\int_a^{500} 1.5 a \mathrm{~d} x+\int_{300}^a(2 x-0.5 a) \mathrm{d} x\right) \\ & =\frac{1}{200}\left(-a^2+900 a-300^2\right) . \end{aligned} \]

所以当 $a=450$ 时可以获利最大。

随机变量函数的数学期望，随机变量函数的分布《知识点总结》的 $\S 2.2$

t20

试证: 对任意的常数 $c \neq E(X)$, 有 \[ \operatorname{Var}(X)=E(X-E(X))^2<E(X-c)^2 . \]

解析

常用的技巧：加一项减一项 \[ E(X-E(X))^2=E[(X-c)-(E(X)-c)]^2=E(X-c)^2-(E(X)-c)^2, \]

由于 $c \neq E(X)$, 所以 $(E(X)-c)^2>0$, 由此得 \[ \operatorname{Var}(X)=E(X-E(X))^2<E(X-c)^2 . \]

t21

已知某商场一天来的顾客数 $X$ 服从参数为 $\lambda$ 的泊松分布, 而每个来到商场的顾客购物的概率为 $p$，每个顾客是否购买商品间相互独立。证明: 此商场一天内购物的顾客数服从参数为 $\lambda p$ 的泊松分布.

解析

用 $Y$ 表示商场一天内购物的顾客数, 则由全概率公式知, 对任意正整数 $k$ 有 \[ \begin{aligned} P(Y=k) & =\sum_{i=k}^{\infty} P(X=i) P(Y=k \mid X=i)=\sum_{i=k}^{\infty} \frac{\lambda^i \mathrm{e}^{-\lambda}}{i!}\binom{i}{k} p^k(1-p)^{i-k} \\ & =\frac{(\lambda p)^k}{k!} \mathrm{e}^{-\lambda} \sum_{i=k}^{\infty} \frac{[\lambda(1-p)]^{i-k}}{(i-k)!} \\ &=\frac{(\lambda p)^k}{k!} \mathrm{e}^{-\lambda} \mathrm{e}^{\lambda(1-p)}\\ &=\frac{(\lambda p)^k}{k!} \mathrm{e}^{-\lambda p} . \end{aligned} \] $ps:$ 第一行到第二行的处理过程是因为要证明服从参数为 $\lambda p$ 的泊松分布，所以凑出来和这个分布对应的系数。

全概率公式、随机变量的独立性、常用离散分布《知识点总结》的 $\S 1.4、1.5、2.4$

t22

设一个人一年内患感冒的次数服从参数 $\lambda=5$ 的泊松分布. 现有某种预防感冒的药物对 $75 \%$ 的人有效 (能将泊松分布的参数减少为 $\lambda=3$ ), 对另外的 $25 \%$ 的人不起作用. 如果某人服用了此药,一年内患了两次感冒, 那么该药对他 (她) 有效的可能性是多少?

解析

根据题干信息肯定需要通过条件概率来修正概率，关键是找到 $P(A \mid B)$ 中的事件 $A$ 和 $B$

根据题干所求信息，容易得到 $A$ 的含义为该药有效；而这个 $B$ 即修正条件是“服药后一年感冒了两次”，所以：

记事件 $B$ 为“服用此药后,一年感冒两次”, 事件 $A$ 为“服用此药后有效”. \[ P(A \mid B)=\dfrac{P(B)P(A\mid B)}{P(A)P(B\mid A)+P(\bar{A})P(B\mid \bar{A})}=\frac{0.75 \times \frac{3^2}{2!} \mathrm{e}^{-3}}{0.75 \times \frac{3^2}{2!} \mathrm{e}^{-3}+0.25 \times \frac{5^2}{2!} \mathrm{e}^{-5}}=0.889 . \]

贝叶斯公式、常用离散分布《知识点总结》的 $\S 1.5、2.4$

t23

设随机变量 $X \sim N\left(108,3^2\right)$ ，求： (1) $P(102 \leq X \leq 117)$ (2) 求 $a$ ，使 $P(X<a)\geqslant0.95$.

解析

（1）： \[ \begin{aligned} P(102 \leqslant X \leqslant 117) & =P\left(\frac{102-108}{3} \leqslant \frac{X-108}{3} \leqslant \frac{117-108}{3}\right)=P\left(-2 \leqslant \frac{X-108}{3} \leqslant 3\right) \\ & =\Phi(3)-\Phi(-2)\\ &=\Phi(3)-[1-\Phi(2)]=0.9987- [1-0.9772]\\&=0.9795 . \\ \end{aligned} \] （2）： \[ \begin{aligned} P(X<a) & =P\left(\frac{X-108}{3}<\frac{a-108}{3}\right)=\Phi\left(\frac{a-108}{3}\right)\geqslant0.95 \\ \Phi(1.645) & \approx 0.95 \\ \Rightarrow a &\geqslant 112.935 \end{aligned} \] 正态分布的概率计算《知识点总结》的 $\S 2.5$

t24

某种圆盘的直径在区间 $(a, b)$ 上服从均匀分布, 试求此种圆盘的平均面积.

解析

记 $X$ 为圆盘的直径, 则圆盘的面积为 $Y=\pi X^2 / 4$, 所以平均面积为 \[ E(Y)=\frac{\pi}{4} E\left(X^2\right)=\frac{\pi}{4}\left[\frac{(b-a)^2}{12}+\frac{(a+b)^2}{4}\right]=\frac{\pi}{12}\left(a^2+b^2+a b\right) . \]

利用方差和期望的关系，通过背诵均匀分布的期望和方差快速得到答案。《知识点总结》的 $\S 一定要背诵的常用概率分布数学期$ $望和方差$

t25

设某种商品每周的需求量 $X$ 服从区间 $(10,30)$ 上均匀分布, 而商店进货数为区间 $(10,30)$ 中的某一整数, 商店每销售 1 单位商品可获利 $500$ 元; 若供大于求则降价处理, 每处理 1 单位商品亏损 $100$ 元; 若供不应求, 则可从外部调剂供应, 此时每 1 单位商品仅获利 $300$ 元. 为使商店所获利润期望值不少于 $9280$ 元, 试确定最少进货量.

解析

设进货量为 $a$, 则利润为 \[ \begin{aligned} g(X) & =\left\{\begin{array}{l} 500 X-100(a-X), \quad 10 \leqslant X \leqslant a, \\ 500 a+300(X-a), \quad a<X \leqslant 30 \end{array}\right. \\ & = \begin{cases}600 X-100 a, & 10 \leqslant X \leqslant a, \\ 300 X+200 a, & a<X \leqslant 30 .\end{cases} \end{aligned} \]

所以平均利润为 \[ \begin{aligned} E(g(X)) & =\int_{10}^{30} g(x) \frac{1}{20} \mathrm{~d} x=\frac{1}{20} \int_{10}^a(600 x-100 a) \mathrm{d} x+\frac{1}{20} \int_a^{30}(300 x+200 a) \mathrm{d} x \\ & =-7.5 a^2+350 a+5250 . \end{aligned} \]

按照题意要求有 \[ -7.5 a^2+350 a+5250 \geqslant 9280 \text { 即 }-7.5 a^2+350 a-4030 \geqslant 0, \]

解得 \[ 20 \frac{2}{3} \leqslant a \leqslant 26, \]

因此最少进货为 21 单位.

是 $t19$ 的类似题。

t26

某种设备的使用寿命 $X$ (以年计) 服从指数分布, 其平均寿命为 $4$ 年.制造此种设备的厂家规定, 若设备在使用一年之内损坏, 则可以予以调换. 如果设备制造厂每售出一台设备可赢利 $100$ 元，而调换一台设备制造厂需花费 $300$ 元. 试求每台设备的平均利润.

解析

根据设备寿命 $X$ 服从指数分布，其平均寿命为 $4$ 年，这说的就是寿命期望 $E(X)=4$ ，根据指数分布 $Exp(\lambda)$ 数学期望为 $\dfrac{1}{\lambda}$ 得到使用寿命服从参数为 $\dfrac{1}{4}$ 的指数分布。 \[ p(x)=\left\{\begin{array}{r} \dfrac{1}{4}e^{-\frac{1}{4}x},x\geqslant0 \\ 0,x<0 \end{array}\right. \] 所以一年内损坏的概率为 \[ P(X\leqslant1)=\int_0^1\dfrac{1}{4}e^{-\frac{1}{4}x}dx=1-e^{-\frac{1}{4}}=0.2212 \] 所以一台机器平均利润 $Y$ 为： \[ E(Y)=100+P(X\leqslant1)(-300)=33.64 \]

t27

已知随机变量 $X$ 的密度函数为 \[ p(x)=\frac{2}{\pi} \cdot \frac{1}{\mathrm{e}^x+\mathrm{e}^{-x}}, \quad-\infty<x<\infty . \]

试求随机变量 $Y=g(X)$ 的概率分布, 其中 \[ g(x)=\left\{\begin{aligned} -1, & \text { 当 } x<0, \\ 1, & \text { 当 } x \geqslant 0 . \end{aligned}\right. \]

解析

因为 $p(x)$ 为偶函数, 所以可得 $P(X<0)=P(X \geqslant 0)=0.5$. 由此得 \[ P(Y=-1)=P(X<0)=P(X \geqslant 0)=P(Y=1)=0.5 . \]

所以 $Y$ 的分布列为 \[ \begin{array}{c|cc} \hline Y & -1 & 1 \\ \hline P & 0.5 & 0.5 \\ \hline \end{array} \]

t28

设随机变量 $X \sim U(0,1)$, 试求 $1-X$ 的分布.

解析

$X$ 的密度函数为 \[ p_X(x)= \begin{cases}1, & 0<x<1, \\ 0, & \text { 其他. }\end{cases} \]

因为 $y=g(x)=1-x$ 在 $(0,1)$ 上为严格单调减函数, 其反函数为 $x=h(y)=1-y$,且有 $h^{\prime}(y)=-1$, 所以 $Y=1-X$ 的密度函数为 \[ p_Y(y)=\left\{\begin{array}{cl} p_X(1-y)|-1|, & 0<y<1, \\ 0, & \text { 其他 } \end{array}= \begin{cases}1, & 0<y<1, \\ 0, & \text { 其他. }\end{cases}\right. \]

这表明: 当 $X \sim U(0,1)$ 时, $1-X$ 与 $X$ 同分布.

采用公式法求解连续随机变量密度函数，《知识点总结》的 $\S2.6$

t29

设随机变量 $\mathrm{X}$ 服从指数分布, 其概率为 $f(x)=\left\{\begin{array}{cl}2 e^{-2 x}, & x>0, \\ 0, & \text { 其他, }\end{array}\right.$

证明:$Y=1-e^{-2 X}$ 在区间 $(0,1)$ 上服从均匀分布.

解析

方法一：

由随机变量 $X$ 的概率密度函数可推之 \[ F_X(x)=\left\{\begin{array}{cc} 1-e^{-2 x}, & x \geq 0, \\ 0, & x<0, \end{array}\right. \] 当 $x>0$ 时, $0<1-e^{-2 x}<1$ 综上 $y \leq 0, F_Y(y)=0 ; y \geq 1, F_Y(y)=1$ 当 $0<y<1$ 时, $F_Y(y)=P\{Y \leq y\}=P\left\{1-e^{-2 X} \leq y\right\}$ \[ =P\left\{X \leq-\frac{1}{2} \ln (1-y)\right\}=F_X\left(-\frac{1}{2} \ln (1-y)\right)=y \]

综上: \[ F_Y(y)=\left\{\begin{array}{lc} 0, & x<0, \\ y, & 0 \leq x<1, \\ 1, & x \geq 1, \end{array}\right. \]

求导得: \[ f_Y(y)=\frac{\mathrm{d}}{\mathrm{d} y} F_Y(y)=\left\{\begin{array}{cc} 1, & 0<x<1, \\ 0, & \text { 其他. } \end{array}\right. \] 方法二：

由于 $X$ 在 $X\geqslant0$ 取值，所以 $Y=1-e^{-2X}$ 的取值范围是 $(0,1]$

$Y=1-e^{-2 X}$ 是严格单调递增的函数，其反函数为 $h(y)=-\dfrac{1}{2}\ln(1-y)$ ，对反函数求导：$h^{\prime}(y)=\dfrac{1}{2(1-y)}$

直接带公式有 \[ f_Y(y)=\left\{\begin{array}{cc} f_X(-\dfrac{1}{2}\ln(1-y))|h^\prime(y)|, & 0<y<1 ， \\ 0, & \text { 其他. } \end{array}\right.=\left\{\begin{array}{cc} 1, & 0<y<1 ， \\ 0, & \text { 其他. } \end{array}\right. \]

t30

设 $X \sim N\left(\mu, \sigma^2\right)$, 求 $Y=\mathrm{e}^X$ 的概率密度函数 $p_Y(y)$.

解析

因为 $Y=\mathrm{e}^X$ 的可能取值范围为 $(0, \infty)$, 且 $y=g(x)=\mathrm{e}^x$ 为严格单调增函数, 其反函数为 $x=h(y)=\ln y$, 及 $h^{\prime}(y)=1 / y$, 所以 $Y$ 的密度函数为 \[ p_Y(y)=\left\{\begin{array}{cc} p_X(\ln y)\left|\dfrac{1}{y}\right|, & y>0, \\ 0, & \text { 其他 } \end{array}= \begin{cases}\dfrac{1}{\sqrt{2 \pi} y \sigma} \exp \left\{-\dfrac{(\ln y-\mu)^2}{2 \sigma^2}\right\}, & y>0, \\ 0, & \text { 其他. }\end{cases}\right. \]

t31

设随机变量 $X \sim N\left(10,2^2\right)$ ，求 $Y=3 X+5$ 的分布

设随机变量 $X \sim N\left(0,2^2\right)$ ，求 $Y=-X$ 的分布

解析

（1）：$Y\sim N(35,6^2)$

（2）：$Y\sim N(0,2^2)$

$ps:$ 设随机变量 $X$ 服从正态分布 $N\left(\mu, \sigma^2\right)$, 则当 $a \neq 0$ 时, 有 $Y=a X+b \sim$ $N\left(a \mu+b, a^2 \sigma^2\right)$

t32

设 $X \sim N\left(0, \sigma^2\right)$, 求 $Y=X^2$ 的分布.

解析

因为 $Y=X^2$ 的可能取值区间为 $(0, \infty)$, 所以当 $y \leqslant 0$ 时, $Y$ 的密度函数为 $p_Y(y)=0$.

而当 $y>0$ 时, $Y$ 的分布函数为 \[ \begin{aligned} F_Y(y)&=P_Y(Y \leqslant y)=P_X\left(X^2 \leq y\right)=P_X(-\sqrt{y} \leq X \leq \sqrt{y}) \\ & =2 \int_0^{\sqrt{y}} \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{x^2}{2 \sigma^2}} d x \\ & =\frac{2}{\sqrt{2 \pi} \sigma} \int_0^{\sqrt{y}} e^{-\frac{x^2}{2 \sigma^2}} d x \\ p_Y(y)&=\frac{d}{d y} F_Y(y)=\frac{2}{\sqrt{2 \pi} \sigma} \cdot \frac{1}{2 \sqrt{y}} \cdot e^{-\frac{y}{2 \sigma^2}} \\ & =\frac{1}{\sqrt{2 \pi y} \sigma} \exp \left\{-\frac{y}{2 \sigma^2}\right\} \\ & \end{aligned} \] 综上， \[ p_Y(y)= \begin{cases}\dfrac{1}{\sqrt{2 \pi y} \sigma} \exp \left\{-\dfrac{y}{2 \sigma^2}\right\}, & y>0, \\ 0, & \text { 其他. }\end{cases} \]

t33

设随机变量 $X$ 的密度函数为 \[ p_X(x)= \begin{cases}\dfrac{2 x}{\pi^2}, & 0<x<\pi, \\ 0, & \text { 其他. }\end{cases} \]

求 $Y=\sin X$ 的密度函数 $p_Y(y)$.

解析

由于 $X$ 在 $(0,\pi)$ 取值，所以 $Y=\sin X$ 的取值范围是 $(0,1)$

当 $0<Y<1$ 时：$F_Y(y)=P_Y(Y \leq y)=P_X(\sin X \leq y)$ $X$ 的积分区间如下：

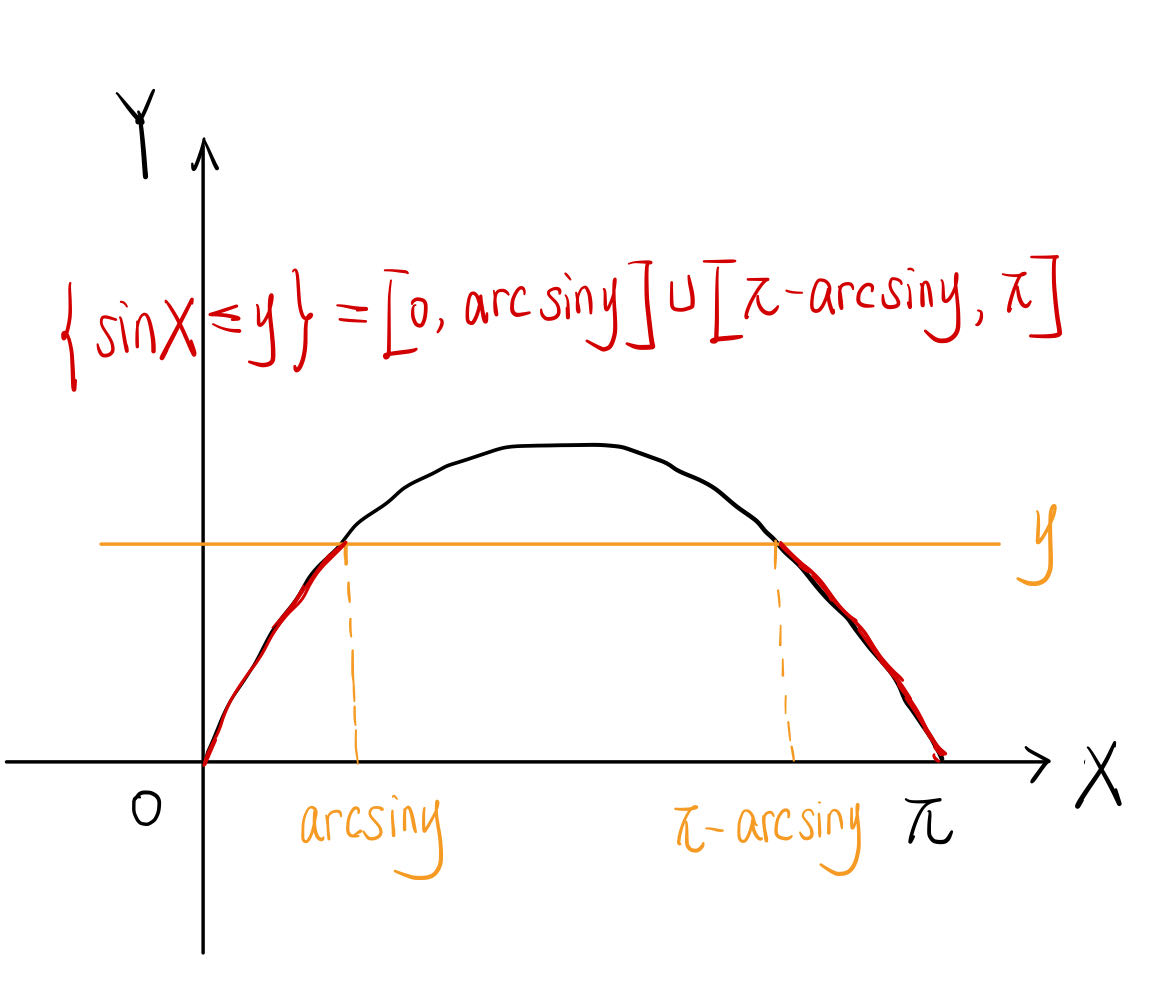\[ \begin{aligned} F_Y(y) & =P(Y \leqslant y)=P(\sin X \leqslant y) \\ & =P(0 \leqslant X \leqslant \arcsin y)+P(\pi-\arcsin y \leqslant X \leqslant \pi) \\ & =\int_0^{\arcsin y} \frac{2 x}{\pi^2} d x+\int_{\pi-\arcsin y} \frac{2 x}{\pi^2} d x \\ P_Y(y) & =\frac{2 \arcsin y}{\pi^2} \cdot \frac{1}{\sqrt{1-y^2}}+\frac{2(\pi-\arcsin y)}{\pi^2 \sqrt{1-y^2}}=\frac{2}{\pi \sqrt{1-y^2}} \\ P_Y(y) & =\left\{\begin{array}{cl} \dfrac{2}{\pi \sqrt{1-y^2}}, & 0<y \leqslant 1 \\ 0, & \left.{(其他}\right) \end{array}\right. \end{aligned} \]

$ps:$ 如果函数 $f(x)$ 连续， $\phi(x)$ 和 $\varphi(x)$ 可导，那么变限积分函数的求导公式可表示为 \[ \Phi^{\prime}(x)=\frac{d}{d x} \int_{\phi(x)}^{\varphi(x)} f(t) d t=f[\varphi(x)] \varphi^{\prime}(x)-f[\phi(x)] \phi^{\prime}(x) \] 当然，如果忘记这个公式，可以硬算出 $F_Y(y)$ 后再求导。

t34

设随机变量 $X$ 的密度函数为 \[ P_X(x)= \begin{cases}\dfrac{1}{2}, & -1<x<0 \\ \dfrac{1}{4}, & 0 \leqslant x<2 \\ 0, & \text { 其他. }\end{cases} \]

求 $Y=X^2$ 的密度函数 $P_Y(y)$ .

解析

从别处看到一个写的很清楚的解析，直接放在下面：

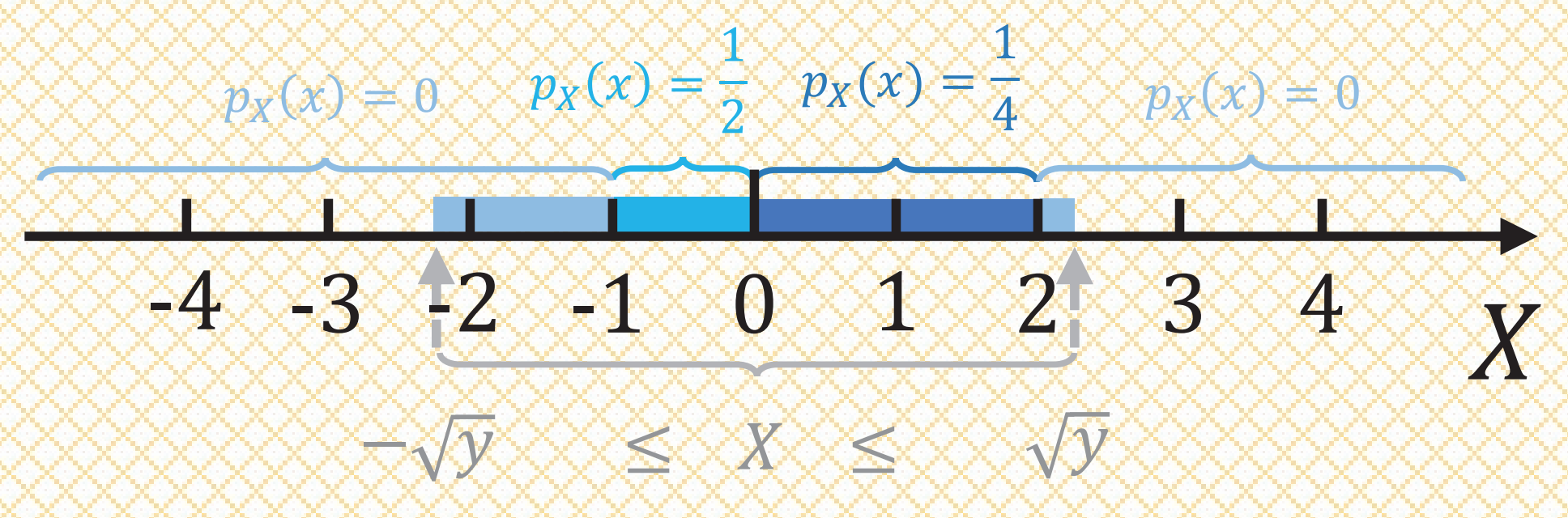
t35

设随机变量 $X \sim U(0,4)$ ，求 $Y=X^2-2 X-3$ 的密度函数 $P_Y(y)$.

解析

$X$ 的在 $(0,4)$ 取值，则 $Y=X^2-2X-3=(X-1)^2-4$ 的取值范围是 $[-4,5)$

所以当 $-4\leq Y <5$ 时：$F_Y(y)=P_Y(Y\leq y)=P_X((X-1)^2\leq y+4)=P_X(1-\sqrt{y+4}\leq X\leq 1+\sqrt{y+4})$

此时要注意：$1-\sqrt{y+4}$ 的取值范围是 $(-2,1)$ 所以要继续将 $Y$ 的取值分成 $(-4,-3)$ 和 $(-3,5)$ 分成两段考虑：

当 $-4<Y<-3$ 时： \[ \begin{aligned} & 0<-\sqrt{y+4}+1<1, \quad 1<\sqrt{y+4}+1<2 \\ & F_Y(y)=\int_{-\sqrt{y+4}+1}^{\sqrt{y+4}+1} \frac{1}{4} d x \Rightarrow p_Y(y)=\frac{1}{4} (y+4)^{-\frac{1}{2}} \end{aligned} \] 当 $-3<Y<5$ 时： \[ \begin{aligned} &-\sqrt{y+4}+1 \leqslant 0,2 \leqslant \sqrt{y+4}+1<4 \\ & F_Y(y)=\int_0^{\sqrt{y+4}+1} \frac{1}{4} d x \Rightarrow p_Y(y)=\frac{1}{8} (y+4)^{-\frac{1}{2}} \end{aligned} \] 综上： \[ p_Y(y)=\left\{\begin{array}{cc} \dfrac{1}{4}(y+4)^{-\frac{1}{2}}, & -4\leqslant y<-3 \\ \dfrac{1}{8}(y+4)^{-\frac{1}{2}}, & -3 \leqslant y<5 \\ 0, & \text { 其他 } \end{array}\right. \]

$t17、t27-t35$ 都是随机变量函数的分布问题，需要熟练掌握公式法和分布函数法，对应知识在《知识点总结》的 $\S 2.6$