概率论习题(1)
t1
解析
A:\(P(A \cup B)=P(A)+P(B)-P(A B)\) 由此推出 \(P(AB)=0\) 无法推出目标条件,错误;
B:这是事件独立的充分必要条件,无法推出目标条件,错误;
C:事件有运算关系:\(A-B=A-A B=A \bar{B}\) ,所以有:
\(P(A\bar{B})=P(A-B)=P(A)-P(AB)\) , \(P(\bar{A}B)=P(B-A)=P(B)-P(AB)\) 又 \(P(A\bar{B})=P(\bar{A}B)\)
由此推出 \(P(A)=P(B)\) ,正确;
D:\(P(\bar{A} \bar{B})=P(\overline{A \cup B})=1-P(A \cup B)=1-P(A)-P(B)+P(A B)\)
由此推出 \(P(A)+P(B)=1\) ,无法推出目标条件,错误。
《知识点总结》的 \(\S1.1、1.3\)
答案
\(C\)
t2
解析
(1):\(A B C \cup \bar{A} \bar{B} \bar{C}\)
(2):\(\bar{A} \bar{B} \bar{C} \cup A\bar{B}\bar{C} \cup \bar{A} B \bar{C} \cup \bar{A} \bar{B} C\)
(3):唯一不符合的情况是 \(ABC\) 同时发生,所以可以写为 \(\Omega-ABC=\overline{ABC}=\bar{A} \cup \bar{B} \cup \bar{C}\)
(4):\(AB\cup AC \cup BC\)
有运用德摩根律,《知识点总结》的 \(\S1.1\)
t3
投掷3颗骰子,求以下事件的概率
(1)所得的最大点数小于等于5;
(2)所得的最大点数等于5。
解析
记 \(Y\) 为所得的最大点数,则
(1)\(P\{Y\leqslant5\}=\dfrac{5^3}{6^3}=\dfrac{125}{126}\)
(2)\(P(Y=5)=P\{Y\leqslant5\}-P\{Y\leqslant4\}=\dfrac{5^3-4^3}{6^3}=\dfrac{61}{216}\)
t4
把 \(n\) 个 “ 0 ” 与 \(n\) 个 “ 1 ” 随机地排列, 求没有两个 “ 1 ” 连在一起的概率.
解析
\(n\) 个 “ \(1\) ” 的放法: \(2 n\) 个位置上 “ \(1\) ” 占有 \(n\) 个位置, 所以共有 \(\displaystyle \binom{2 n}{n}\) 种放法,这是总的放法,即分母。
“没有两个 1 连在一起”, 相当于在 \(n\) 个 “ \(0\) ” 之间及两头 (共 \(n+1\) 个位置)去放 \(1\) ,所以有 \(\displaystyle \binom{n+1}{n}\) 种放法。
综上,答案为:\(p_n=\dfrac{\displaystyle \binom{n+1}{n}}{\displaystyle\binom{2 n}{n}}=\dfrac{n+1}{\displaystyle\binom{2 n}{n}}\).
拓展
问:把 \(n\) 个完全相同的球随机地放到 \(N\) 个盒子中,有多少种情况?
答:用 \(N+1\) 根火柴棒来表示 \(N\) 个盒子,因为球要放到盒子中间,所以最旁边的两根火柴棒的外面不可以放球,所以自由移动的球和火柴棒的位置为 \(n+N+1-2=N+n-1\) 个,挑出 \(n\) 个位置放球,最终答案为:\(\displaystyle \binom{N+n-1}{n}\)
这个也称为排列组合里的重复组合。
t5
抽样模型:设 \(N\) 件产品中有 \(M\) 件是次品, \(N-M\) 件是正品。现从 \(N\) 件中随机地不放回地抽取 \(n\) 件产品。求:
事件 \(A_m=\{\) 所取的 \(n\) 件产品中恰有 \(m\) 件次品 \(\}\) 的概率. \(m=0,1,2,\cdots,n\)
解析
\[ P\left(A_m\right)=\dfrac{\displaystyle \binom{N-M}{n-m} \displaystyle \binom{M}{m}}{\displaystyle \binom{N}{n}} \]
拓展
现在为有放回地抽取,则新的概率为 \[ P\left(A_m\right)=\displaystyle \binom{n}{m}\left(\dfrac{M}{N}\right)^m\left(1-\dfrac{M}{N}\right)^{n-m} \]
t6
盒子模型:设有 \(n\) 个(不同)球, 每个球等可能地落入 \(N\) 个不同的盒子中 \((n \leq N)\),设每个盒子容球数不限, 求下列事件的概率:
\(A=\) “指定的 \(n\) 个盒子中各有一球”;
\(B=\) “恰有 \(n\) 个盒子中各有一球”.
解析
(1)\(P(A)=\dfrac{n!}{N^n}\)
(2)\(P(B)=\dfrac{C_N^n n!}{N^n}=\dfrac{N!n!}{(N-n)!n!N^n}=\dfrac{N!}{(N-n)!N^n}\)
t7
抽签模型:袋中有 \(a\) 只白球, \(b\) 只红球, 它们除颜色不同外,其他方面没有差别,现在把球随机地一只只摸出来, 作
(1)放回取样;
(2)不放回取样;
求第 \(k\) 次摸出的球是白球的概率 \((k \leq a+b)\)
解析
(1)\(p_k=\dfrac{a}{a+b}\)
(2)样本空间包含样本点的总数为: \(P_{a+b}^k\) (排列)
第 \(k\) 个球为白球事件的总数为:\(C_a^1P_{a+b-1}^{k-1}\) \[ \Rightarrow P_k=\frac{a \times P_{a+b-1}^{k-1}}{P_{a+b}^k}=\frac{a \times(a+b-1) \cdots(a+b-k+1)}{(a+b) \cdots(a+b-k+1)}=\frac{a}{a+b} \]
\(t5-t7\) 均为古典概型,《知识点总结》的 \(\S1.2\)
t8
甲乙两艘轮船驶向一个不能同时停泊两艘轮船的码头, 它们在一昼夜内到达的时间是等可能的. 如果甲船的停泊时间是 1 小时, 乙船的停泊时间是 2 小时, 求它们中任何一艘都不需要等候码头空出的概率是多少?
解析
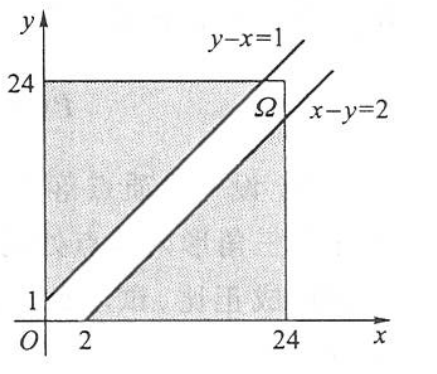
如上图所示,记 \(x\) 和 \(y\) 分别为甲乙两艘轮船到达码头的时间。
则 \(p=\dfrac{S_A}{S_\Omega}=\dfrac{\frac{1}{2}(23^2+22^2)}{24^2}=0.879\)
\(t8\) 均为几何概型,《知识点总结》的 \(\S1.2\)
t9
设随机事件 \(A, B\) 相互独立, \(A, C\) 相互独立, \(B C=\varnothing\) 若\(P(A)=P(B)=\frac{1}{2}, P(A C \mid A B \cup C)=\frac{1}{4}\)
求 \(P(C)\)
解析
\[ \begin{aligned} P(A C \mid A B \cup C) & =\frac{P[A C \cap(A B \cup C)]}{P(A B \cup C)}=\frac{P(A B C \cup A C)}{P(A B)+P(C)-P(A B C)} \\ & =\frac{P(A C)}{P(A B)+P(C)-P(A B C)}\\ & =\frac{P(A)P(C)}{P(A)P(B)+P(C)-0}\\ & =\dfrac{\frac{1}{2}P(C)}{\frac{1}{2}\frac{1}{2}+P(C)}\\ & =\frac{1}{4} \end{aligned} \]
解得:\(P(C)=\dfrac{1}{4}\)
条件概率与事件独立性、还有事件之间的运算,《知识点总结》的 \(\S1.1、1.3、1.4、1.5\)
t10
匹配问题:某人写好 \(n\) 封信,又写好 \(n\) 只信,然后在黑暗中把每封信放入一只信封中, 试求至少有一封信放对的概率。
解析
记 \(A_k\) 表示第 \(k\) 封信放对了。 \[ \begin{aligned} P&=P\left(A_1 \cup A_2 \cup \cdots \cup A_n\right)=\sum P\left(A_i\right)-\sum P\left(A_i A_j\right)+\sum\left(A_i A_j A_k\right)+\cdots+(-1)^{n-1} \sum\left(A_1 A_2 \cdots A_n\right) \\ &其中:\\ & P\left(A_i\right)=\frac{(n-1)!}{n!}=\frac{1}{n} \\ & P\left(A_i A_j\right)=\frac{(n-2)!}{n!}=\frac{1}{n(n-1)} \\ & \cdots \\ P&=\binom{n}{1} \frac{1}{n}-\binom{n}{2} \frac{1}{n(n-1)}+\binom{n}{3} \frac{1}{n(n-1)(n-2)}+\cdots+(-1)^{n-1} \frac{1}{n!} \\ & =1-\frac{1}{2!}+\frac{1}{3!}-\cdots+(-1)^{n-1} \frac{1}{n!} \end{aligned} \]
t11
已知 \(P(\bar{A})=0.3, P(B)=0.4, P(A \bar{B})=0.5\), 求 \(P(B \mid A \cup \bar{B})\).
解析
\[ \begin{aligned} &P(B \mid A \cup \bar{B})=\frac{P(A B)}{P(A \cup \bar{B})}, \\ &P(A \cup \bar{B})=P(A)+P(\bar{B})-P(A \bar{B})=0.7+0.6-0.5=0.8 . \\ &P(A\bar{B})=P(A)-P(A B) \text {, 可得 } P(A B)=P(A)-P(A \bar{B})=0.7-0.5=0.2\\ &P(B \mid A \cup \bar{B})=\frac{P(A B)}{P(A \cup \bar{B})}=\frac{0.2}{0.8}=0.25 . \end{aligned} \]
条件概率与事件之间的运算,《知识点总结》的 \(\S1.1、1.3、1.4\)
t12
\(m\) 个人相互传球, 球从甲手中传出, 每次传球时, 传球者等可能地把球传给其余 \(m-1\) 个人中的任何一个, 求第 \(n\) 次传球时仍由甲传出的概率。
解析
\[ \begin{aligned} &\text {设} A_i \text {为第i以次甲传出} \Rightarrow P\left(A_n\right)=P\left(A_{n-1}\right) P\left(A_n \mid A_{n-1}\right)+P\left(\bar{A}_{n-1}\right) P\left(A_n \mid \bar{A}_{n-1}\right)\\ &\Rightarrow P\left(A_n\right)=\frac{1}{m-1} P\left(\bar{A}_{n-1}\right) \\ &\Rightarrow P\left(A_n\right)=\frac{1}{m-1}\left(1-P\left(A_{n-1}\right)\right) \quad\text {一阶线性递推数列} \\ &\text{上述等式一定可以化成这样的形式:} P\left(A_n\right)-M=N\left[P\left(A_{n-1}\right)-M\right] \\ &\text {对比系数:} N=-\frac{1}{m-1}, M=\frac{1}{m} \\ &P\left(A_n\right)-\frac{1}{m}=\frac{1}{1-m}\left(P\left(A_{n-1}\right)-\frac{1}{m}\right) \quad P\left(A_1\right)=1 \\ &\text {令} P\left(A_n\right)-\frac{1}{m}=b_n \\ &\quad b_n=\frac{1}{1-m} \cdot b_{n-1}=\left(\frac{1}{1-m}\right)^2 \cdot b_{n-2}=\cdots=\left(\frac{1}{1-m}\right)^{n-1} \cdot b_1 \\ &\quad=\left(\frac{1}{1-m}\right)^{n-1} \cdot\left(1-\frac{1}{m}\right)=\left(\frac{-1}{m-1}\right)^{n-2} \times \frac{-1}{m} \\ &\Rightarrow P\left(A_n\right)=b_n+\frac{1}{m}=\frac{1}{m}\left[1-\left(\frac{-1}{m-1}\right)^{n-2}\right], n=2,3,4, \cdots \end{aligned} \]
关键在于利用全概率公式划分事件。
线性递推数列求解通项公式可以参考 第零篇 数列递推 | StudyinCAU
t13
盒中装有8个乒乓球,其中有6个新的。第一次练习时,从中任取2个来用,用完后放回盒中。第二次练习时,再从盒中任取2个。求:
(1)第二次取出的球都是新球的概率;
(2)在第二次取出的球都是新球的条件下,第一次取到的球都是新球的概率。
解析
(1)记 \(B\) 为第二次取出的球是2个新球。 \[ P(B)=\frac{C_6^2 C_4^2}{C_8^2 C_8^2}+\frac{C_6^1 C_2^1 C_5^2}{C_8^2 C_8^2}+\frac{C_2^2 C_6^2}{C_8^2 C_8^2}=\frac{225}{784} \] (2)记 \(A\) 为第一次取出的球是2个新球。 \[ P(A \mid B)=\frac{P(A B)}{P(B)}=\frac{C_6^2 C_4^2}{C_8^2 C_8^2} \times \frac{784}{225}=\frac{2}{5} . \]
古典概型、条件概率,《知识点总结》的 \(\S1.2、1.4\)
t14
某人从外地赶来参加会议, 他乘火车、轮船、汽车或飞机来的概率分别为 \(\dfrac{3}{10}, \dfrac{1}{5}, \dfrac{1}{10}, \dfrac{2}{5}\) 如果他乘飞机来, 则不会迟到, 乘火车、轮船或汽车迟到的概率分别为 \(\dfrac{1}{4}, \dfrac{1}{3}, \dfrac{1}{12}\), 试问:
(1)他迟到的概率;
(2)此人迟到, 试推断他乘火车来的概率有多大。
解析
(1)记 \(A\) 为迟到;记 \(B_1\) 为乘火车,\(B_2\) 为乘轮船,\(B_3\) 为乘汽车,\(B_4\) 为乘飞机。 \[ P(A)=\sum_{i=1}^4 P\left(B_i\right) P\left(A \mid B_i\right)=\frac{3}{20} \] (2)\(P\left(B_1 \mid A\right)=\dfrac{P\left(A \mid B_1\right) P\left(B_1\right)}{P(A)}=\dfrac{1}{2}\)