基础知识回顾与拓展(一)
数学知识回顾与拓展(一)
1 线性代数
1.1 向量
在最优化方法的课程中,默认向量为列向量的形式。
\(n\)维列向量定义为包含\(n\)个实数的数组,记作: \[ \boldsymbol{a}=\left[\begin{array}{c}a_1 \\ a_2 \\ \vdots \\ a_n\end{array}\right] \] \(a_i\) 表示向量 \(\boldsymbol{a}\) 的第 \(i\) 个元素。定义 \(\mathbb{R}\) 为全体实数组成的集合,那么由实数组成的 \(n\) 维列向量可表示为 \(\mathbb{R}^n\), 称为 \(n\) 维实数向量空间。通常将 \(\mathbb{R}^n\) 的元素(\(n\)维向量)用小写粗体字母表示 (如 \(\boldsymbol{x}\) )。向量 \(\boldsymbol{x} \in \mathbb{R}^n\) 中的元素记为 \(x_1, \cdots, x_n\) 。
\(n\) 维行向量记为 \(\left[a_1, a_2, \cdots, a_n\right]\), 向量 \(\boldsymbol{a}\) 的转置记为 \(\boldsymbol{a}^T\) 。比如, 如果 \[ \boldsymbol{a}=\left[\begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_n \end{array}\right] \]
那么 \[ \boldsymbol{a}^T=\left[a_1, a_2, \cdots, a_n\right] \]
相应的, 列向量\(\boldsymbol{a}\)可以记为 \(\boldsymbol{a}=\left[a_1, a_2, \cdots, a_n\right]^T\) 。
1.2 线性相关
1.2.1 线性相关与线性无关的定义
如果方程: \[ \alpha_1 \boldsymbol{a}_1+\alpha_2 \boldsymbol{a}_2+\cdots+\alpha_k \boldsymbol{a}_k=\mathbf{0} \]
只有在所有系数 \(\alpha_i(i=1, \cdots, k)\) 都等于零的前提下等号成立, 那么称向量集 \(\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right\}\) 是线性无关的,否则称向量集是线性相关的。
线性相关的一些结论
1.如果集合中只包括一个向量 \(\boldsymbol{0}\), 由于对于任意 \(\alpha \neq 0\), 都有 \(\alpha \mathbf{0}=\mathbf{0}\),因此,该集合是线性相关的。实际上,所有包含零向量的集合都是线性相关的,假设这个集合有\(n\)个向量元素,令剩下的\((n-1)\)个元素\(\alpha_1 \boldsymbol{a}_1+\alpha_2 \boldsymbol{a}_2+\cdots+\alpha_{k-1} \boldsymbol{a}_{k-1}=\mathbf{0}\) ,这些系数可以全部为\(0\),即: \(\alpha_i(i=1, \cdots, k-1)\) 都为\(0\),剩下的零向量前的系数不为 \(0\) 即可,所以所有包含零向量的集合都是线性相关的。 2.如果集合中只包括一个非零向量 : \(\boldsymbol{a} \neq \mathbf{0}\) , 只有 \(\alpha=0\)时, 才有 \(\alpha\boldsymbol{a}=\boldsymbol{0}\) 成立,因此,该集合是线性无关的。
1.2.2 线性组合
给定向量 \(\boldsymbol{a}\), 如果存在标量 \(\alpha_1, \cdots, \alpha_k\), 使得 \[ \boldsymbol{a}=\alpha_1 \boldsymbol{a}_1+\alpha_2 \boldsymbol{a}_2+\cdots+\alpha_k \boldsymbol{a}_k \]
那么称向量 \(\boldsymbol{a}\) 为向量\(\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\) 的线性组合。
定理向量集 \(\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right\}\) 是线性相关的,当且仅当集合中的一个向量可以表示为其他向量的线性组合。
证明:
必要性。如果 \(\left\{a_1, a_2, \cdots, a_k\right\}\) 是线性相关的, 那么有 \[ \alpha_1 \boldsymbol{a}_1+\alpha_2 \boldsymbol{a}_2+\cdots+\alpha_k \boldsymbol{a}_k=\mathbf{0} \]
其中至少存在一个标量 \(\alpha_i \neq 0\), 从而有 \[ \boldsymbol{a}_i=-\frac{\alpha_1}{\alpha_i} \boldsymbol{a}_1-\frac{\alpha_2}{\alpha_i}\boldsymbol{a}_2-\cdots-\frac{\alpha_k}{\alpha_i} \boldsymbol{a}_k \] 充分性。不妨设向量 \(\boldsymbol{a_1}\) 可以被表示为其他向量的线性组合: \[ \boldsymbol{a}_1=\alpha_2 \boldsymbol{a}_2+\alpha_3 \boldsymbol{a}_3+\cdots+\alpha_k \boldsymbol{a}_k \]
那么有 \[ (-1) \boldsymbol{a}_1+\alpha_2 \boldsymbol{a}_2+\cdots+\alpha_k \boldsymbol{a}_k=\mathbf{0} \]
因为第一个标量非零,所以向量集 \(\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right\}\) 是线性相关的。
得证。
1.2.3向量空间
1.2.3.1 子空间
令 \(\mathcal{V}\) 表示 \(\mathbb{R}^n\) 的一个子集, 如果 \(\mathcal{V}\) 在向量加和运算及标量乘积运算下是封闭的,那么称 \(\mathcal{V}\) 为 \(\mathbb{R}^n\) 的一个子空间。
注:每个子空间都包含零向量。
假定 \(\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\) 是 \(\mathbb{R}^n\) 中的任意向量, 它们所有线性组合的集合称为 \(\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\) 张成的子空间。记为: \[ span\left[\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right]=\left\{\sum_{i=1}^k \alpha_i \boldsymbol{a}_i: \alpha_1, \cdots, \alpha_k \in \mathbb{R}\right\} \]
任意向量集合都能张成一个子空间。
1.2.3.2 基
给定子空间 \(\mathcal{V}\) ,如果存在线性无关的向量集合 \(\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right\} \subset \mathcal{V}\) 使得 \(\mathcal{V}=\operatorname{span}\left[\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right]\) ,那么称 \(\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right\}\) 是子空间 \(\mathcal{V}\) 的一组基。子空间 \(\mathcal{V}\) 中的所有基都包含相同数量的向量, 这一数量称为 \(\mathcal{V}\) 的维数, 记为 \(\operatorname{dim} \mathcal{V}\) 。
如果 \(\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right\}\) 是 \(\mathcal{V}\) 的一组基, 那么 \(\mathcal{V}\) 中的任一向量 \(\boldsymbol{a}\) 可以唯一地表示为 \[ \boldsymbol{a}=\alpha_1 \boldsymbol{a}_1+\alpha_2 \boldsymbol{a}_2+\cdots+\alpha_k \boldsymbol{a}_k \]
其中,\(\alpha_i \in \mathbb{R}, i=1,2, \cdots, k\) 。
给定 \(\mathcal{V}\) 的一组基 \(\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right\}\) 和向量 \(\boldsymbol{a} \in \mathcal{V}\) ,如果 \[ \boldsymbol{a}=\alpha_1 \boldsymbol{a}_1+\alpha_2 \boldsymbol{a}_2+\cdots+\alpha_k \boldsymbol{a}_k \]
那么系数 \(\alpha_i, i=1, \cdots, k\) 称为 \(a\) 对应于基 \(\left\{\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_k\right\}\) 的坐标。
\(\mathbb{R}^n\) 的标准基为 \[ \boldsymbol{e}_1=\left[\begin{array}{l}1 \\0 \\0 \\\vdots \\0 \\0\end{array}\right], \boldsymbol{e}_2=\left[\begin{array}{l}0 \\1 \\0 \\\vdots \\0 \\0\end{array}\right], \cdots, \boldsymbol{e}_n=\left[\begin{array}{l}0 \\0 \\0 \\\vdots \\0 \\1\end{array}\right] \]
在标准基下,向量 \(x\) 可表示为 \[ \boldsymbol{x}=\left[\begin{array}{llll}x_1 & x_2 & \cdots & x_n\end{array}\right]^T=x_1 \boldsymbol{e}_1+x_2 \boldsymbol{e}_2+\cdots+x_n \boldsymbol{e}_n \]
1.3 初等变换
对矩阵进行以下三种变换的称为行初等变换
对换两行(对换 \(i, j\) 两行, 记作 \(r_i \leftrightarrow r_j\) );
以数 \(k \neq 0\) 乘某一行中所有的元素(第 \(i\) 行乘 \(k\), 记作 \(r_i \times k\) );
把某一行所有元的 \(k\) 倍, 加到另一行对应的元上去 (第 \(j\) 行的 \(k\) 倍加到第 \(i\) 行上, 记作 \(r_i+k r_j\) ). 矩阵的行初等变换与列初等变换, 统称为矩阵的初等变换。
对一个矩阵每进行一次初等行变换相当于为这个矩阵左乘了一个初等矩阵,初等列变换相当于右乘一个初等矩阵。
1.4 矩阵的秩
矩阵 \(\boldsymbol{A}\) 中线性无关列的最大数目称为 \(\boldsymbol{A}\) 的秩, 记为 \(r a n k \boldsymbol{A}\) 。矩阵 \(A\) 的秩等于它的非零子式的最高阶数。
注:对矩阵进行初等变换不改变矩阵的秩。
如果矩阵 \(\boldsymbol{A}\) 的行数等于列数, 那么该矩阵称为方阵。行列式是与每个方阵相对应的一个标量, 记为 \(\operatorname{det} \boldsymbol{A}\) 或 \(|\boldsymbol{A}|\) 。
如果一个 \(m \times n(m \geq n)\) 矩阵 \(A\) 具有非零的 \(n\) 阶子式,那么 \(A\) 的各列是线性无关的,即 \(r a n k \boldsymbol{A}=n\) 。
1.5 内积与范数
对于 \(\boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^n\), 定义欧式内积为 \[ \langle\boldsymbol{x}, \boldsymbol{y}\rangle=\sum_{i=1}^n x_i y_i=\boldsymbol{x}^T \boldsymbol{y} \]
定义向量 \(\boldsymbol{x}\) 的欧氏范数为 \[ \|\boldsymbol{x}\|=\sqrt{\langle\boldsymbol{x}, \boldsymbol{x}\rangle}=\sqrt{\boldsymbol{x}^T \boldsymbol{x}} \]
向量 \(x\) 的欧氏范数 \(\|x\|\) 具有如下性质:
- 非负性: \(\boldsymbol{x}\) 的欧氏范数 \(\|\boldsymbol{x}\| \geq 0\), 当且仅当 \(\boldsymbol{x}=\boldsymbol{0}\) 时, \(\|\boldsymbol{x}\|=0\)
- 齐次性: \(\|r \boldsymbol{x}\|=|r|\|\boldsymbol{x}\| \geq 0, r \in \mathbb{R}\)
- 三角不等式: \(\|\boldsymbol{x}+\boldsymbol{y}\| \leq\|\boldsymbol{x}\|+\|\boldsymbol{y}\|\)
1.6 求方阵的逆
设 \(\boldsymbol{A}\) 为矩阵, 如果存在 \(n\) 阶方阵 \(\boldsymbol{B}\), 使得: \[ \boldsymbol{A}\boldsymbol{B}=\boldsymbol{B}\boldsymbol{A}=\boldsymbol{I} \] 则称 \(\boldsymbol{A}\)是可逆矩阵, \(\boldsymbol{B}\) 是 \(\boldsymbol{A}\) 的逆矩阵。
定理1如果 \(\boldsymbol{A}\) 是一个 \(n\) 阶可逆矩阵, 则 \(\boldsymbol{A}\) 的逆矩阵是唯一的。
定理2\(n\) 阶方阵 \(\boldsymbol{A}\) 可逆的充分必要条件是行列式 \(|\boldsymbol{A}| \neq 0\)
1.6.1 利用伴随矩阵求方阵的逆
当 \(|\boldsymbol{A}| \neq 0\) 时, \[ \boldsymbol{A}^{-1}=\frac{1}{|\boldsymbol{A}|} \boldsymbol{A}^*=\frac{1}{|\boldsymbol{A}|}\left[\begin{array}{cccc}A_{11} & A_{21} & \cdots & A_{n 1} \\A_{12} & A_{22} & \cdots & A_{n 2} \\\vdots & \vdots & & \vdots \\A_{1 n} & A_{2 n} & \cdots & A n n\end{array}\right] \]
其中 \(\boldsymbol{A}^*\) 是 \(\boldsymbol{A}\) 的伴随阵, \(A_{i j}\) 是 \(a_{i j}\) 的代数余子式, 注意伴随矩阵的行列关系。
1.6.2 \(Gauss-Jordan\)方法
简而言之, \(Gauss-Jordan\)的想法是: 如果我们对 \(\boldsymbol{A}\) 执行一些行操作以获得 \(\boldsymbol{I}\), 那么对 \(\boldsymbol{I}\) 执行相同的行操作会得到 \(\boldsymbol{A^{-1}}\) 。为什么?
行操作对应于从 \(\boldsymbol{A}\) 左边乘以一组矩阵 \(\boldsymbol{E}=\cdots \boldsymbol{E_2 E_1}\)
所以, 对 \(\boldsymbol{A}\) 做行操作将其变成 \(\boldsymbol{I}\) 意思等价于 \(\boldsymbol{E} \boldsymbol{A}=\boldsymbol{I}\), 因此 \(\boldsymbol{E}=\boldsymbol{A^{-1}}\).
对 \(\boldsymbol{I}\) 执行相同的行操作, 相当于 \(\boldsymbol{I}\)左乘矩阵 \(E\), 即 \(E I\), 因为 \(\boldsymbol{E} \boldsymbol{I}=\boldsymbol{E}\) 并且 \(\boldsymbol{E}=\boldsymbol{A^{-1}}\), 所以结果就是 \(\boldsymbol{A^{-1}}\)。这就是我们可以用扩展矩阵来进行高斯消除, 对 \(\boldsymbol{A}\) 和 \(\boldsymbol{I}\) 同时执行相同的行操作, 即:
\[ \left(\begin{array}{ll}\boldsymbol{A} & \boldsymbol{I}\end{array}\right) \underset{\text { row ops }}{\longrightarrow}\left(\begin{array}{ll}\boldsymbol{I} & \boldsymbol{A^{-1}}\end{array}\right) \]
1.7 特征值与特征向量
1.7.1 基本概念与一些结论
令 \(\boldsymbol{A}\) 是 \(n \times n\) 的实数方阵。存在标量 \(\lambda\) (可能为复数) 和非零向量 \(\boldsymbol{v}\) 满足等式: \[ \boldsymbol{A v}=\lambda \boldsymbol{v} \] \(\lambda\) 称为 \(\boldsymbol{A}\) 的特征值, \(\boldsymbol{v}\) 称为 \(\boldsymbol{A}\) 的特征向量。
已知 \(n\) 阶齐次线性方程组 \((\lambda \boldsymbol{I}-\boldsymbol{A}) \boldsymbol{x}=0\) 有非零解的充分必要条件是系数行列式为 \(0\)。即矩阵 \(\lambda \boldsymbol{I}-\boldsymbol{A}\) 有 \(\operatorname{det}[\lambda \boldsymbol{I}-\boldsymbol{A}]=0\), 于是有 \(n\) 次方程成立: \[ \operatorname{det}[\lambda \boldsymbol{I}-\boldsymbol{A}]=\lambda^n+a_{n-1} \lambda^{n-1}+\cdots+a_1 \lambda+a_0=0 \] 多项式 \(\operatorname{det}[\lambda \boldsymbol{I}-\boldsymbol{A}]\) 称为矩阵 \(\boldsymbol{A}\)的特征多项式, 上面的方程称为特征方程。由代数的基本原理可知, 特征方程必定有 \(n\)个根(可能存在相同的根),即为\(\boldsymbol{A}\)的\(n\)个特征值。若 \(\boldsymbol{A}\) 有 \(n\) 个相异的特征值,那么它也有 \(n\)个线性无关的特征向量。
1.7.2 矩阵对角化
设矩阵 \(\boldsymbol{A}\) 为\(n\)阶方阵。考虑其特征向量 \(\left\{\boldsymbol{v}_1, \boldsymbol{v}_2, \cdots, \boldsymbol{v}_n\right\}\) 构成的一组线性无关基。在这一组基下,可对矩阵 \(\boldsymbol{A}\) 进行对角化, 即对所有的 \(i \neq j\), 对角矩阵的第 \((i, j)\) 个元素 \(a_{i j}=\) 0 。令 \[ \boldsymbol{T}=\left[\boldsymbol{v}_1, \boldsymbol{v}_2, \cdots, \boldsymbol{v}_n\right]^{-1} \] 则有: \[ \begin{aligned} \boldsymbol{T A T}^{-1} & =\boldsymbol{T A}\left[\boldsymbol{v}_1, \boldsymbol{v}_2, \cdots, \boldsymbol{v}_n\right] \\ & =\boldsymbol{T}\left[\boldsymbol{A} \boldsymbol{v}_1, \boldsymbol{A} \boldsymbol{v}_2, \cdots, \boldsymbol{A} \boldsymbol{v}_n\right] \\ & =\boldsymbol{T}\left[\lambda_1 \boldsymbol{v}_1, \lambda_2 \boldsymbol{v}_2, \cdots, \lambda_n \boldsymbol{v}_n\right] \\ &=\boldsymbol{T} \boldsymbol{T}^{-1}\left[\begin{array}{llll}\lambda_1 & & & 0 \\& \lambda_2 & & \\& & \ddots & \\0 & & & \lambda_n\end{array}\right] \\ & =\left[\begin{array}{llll}\lambda_1 & & & 0 \\& \lambda_2 & & \\& & \ddots & \\0 & & & \lambda_n\end{array}\right] \end{aligned} \]
定理对于任意 \(n \times n\) 实对称矩阵, 存在 \(n\) 个相互正交的特征向量。
证明:假定 \(\boldsymbol{A} \boldsymbol{v}_1=\lambda_1 \boldsymbol{v}_1, \boldsymbol{A} \boldsymbol{v}_2=\lambda_2 \boldsymbol{v}_2\), 其中 \(\lambda_1 \neq \lambda_2\), 那么有 \[ \boldsymbol{v}_1^T \boldsymbol{A} \boldsymbol{v}_2=\boldsymbol{v}_1^T\left(\boldsymbol{A} \boldsymbol{v}_2\right)=\lambda_2\left(\boldsymbol{v}_1^T \boldsymbol{v}_2\right) \]
根据 \(\boldsymbol{A}=\boldsymbol{A}^T\), 有 \[ \boldsymbol{v}_1^T \boldsymbol{A} \boldsymbol{v}_2=\left(\boldsymbol{v}_1^T \boldsymbol{A}^T\right) \boldsymbol{v}_2=\left(\boldsymbol{A} \boldsymbol{v}_1\right)^T \boldsymbol{v}_2=\lambda_1\left(\boldsymbol{v}_1^T \boldsymbol{v}_2\right) \]
因此, \[ \lambda_1\left(\boldsymbol{v}_1^T \boldsymbol{v}_2\right)=\lambda_2\left(\boldsymbol{v}_1^T \boldsymbol{v}_2\right) \]
由于 \(\lambda_1 \neq \lambda_2\), 可以推出 \[ \left(\boldsymbol{v}_1^T \boldsymbol{v}_2\right)=0 \] 所以特征向量相互正交。
1.8 二次型
1.8.1 二次型函数
设二次型函数 \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) 定义为具有如下形式的函数: \[ f(\boldsymbol{x})=\boldsymbol{x}^T \boldsymbol{Q} \boldsymbol{x} \]
其中 \(\boldsymbol{Q}\) 是一个 \(n \times n\) 实数矩阵。 \[ \begin{aligned}f(\boldsymbol{x}) & =q_{11} x_1^2+q_{12} x_1 x_2+\cdots+q_{1 n} x_1 x_n \\& +q_{21} x_2 x_1+q_{22} x_2^2+\cdots+q_{2 n} x_2 x_n \\& +\cdots \\& +q_{n 1} x_n x_1+q_{n 2} x_2^2+\cdots+q_{n n} x_n^2 \\& =\left[x_1, x_2, \cdots, x_n\right]\left[\begin{array}{cccc}q_{11} & q_{12} & \cdots & q_{1 n} \\q_{21} & q_{22} & \cdots & q_{2 n} \\\vdots & \vdots & \vdots & \vdots \\q_{n 1} & q_{n 2} & \cdots & q_{n n}\end{array}\right]\left[\begin{array}{c}x_1 \\x_2 \\\vdots \\x_n\end{array}\right]\\&=\boldsymbol{x}^T \boldsymbol{Q} \boldsymbol{x}\end{aligned} \]
1.8.2 正定
当对于任一非零向量 \(\boldsymbol{x}\), 都有 \(\boldsymbol{x}^T \boldsymbol{Q x}>0\), 则二次型 \(\boldsymbol{x^T} \boldsymbol{Q}\boldsymbol{x}\) 是正定的, 若 \(\boldsymbol{x^T} \boldsymbol{Q}\boldsymbol{x} \geq 0\) 则此二次型是半正定。类似的, \(\boldsymbol{x}^T \boldsymbol{Q x}<0\), 或者 \(\boldsymbol{x^T} \boldsymbol{Q}\boldsymbol{x} \leq 0\) 则说明二次型是负定或半负定的。
矩阵 \(\boldsymbol{Q}\) 的顺序主子式为 \(\operatorname{det} \boldsymbol{Q}\) 自身以及从矩阵 \(\boldsymbol{Q}\) 中依次移除最后一行和最后一列获得的所有子式, 即: \[ \begin{aligned} & \Delta_1=q_{11}, \quad \Delta_2=\left[\begin{array}{ll}q_{11} & q_{12} \\q_{21} & q_{22}\end{array}\right] \\ & \Delta_3=\operatorname{det}\left[\begin{array}{lll}q_{11} & q_{12} & q_{13} \\q_{21} & q_{22} & q_{23} \\q_{31} & q_{32} & q_{33}\end{array}\right], \cdots, \Delta_n=\operatorname{det} \boldsymbol{Q} \\ \end{aligned} \]
定理1给定二次型 \(\boldsymbol{x}^T \boldsymbol{Q} \boldsymbol{x}\) ,其中 \(\boldsymbol{Q}=\boldsymbol{Q}^T\), 该二次型是正定的,当且仅当的 \(Q\) 顺序主子式是正定的。
定理2对称矩阵 \(\boldsymbol{Q}\) 是正定(半正定)的, 当且仅当 \(\boldsymbol{Q}\) 的所有特征值是正的 (非负的)。
2 线段与超平面
2.1 线段
对于 \(n\) 维向量 \(\boldsymbol{x}=\left[x_1, x_2, \cdots, x_n\right]^T, \quad \boldsymbol{y}=\left[y_1, y_2, \cdots, y_n\right]^T\), 两点之间的所有点的集合称为两点之间的线段。如果 \(z\) 在这条线段上,那么有 \[ \boldsymbol{z}=\boldsymbol{y}+\alpha(\boldsymbol{x}-\boldsymbol{y})\quad\alpha\in[0,1] \] 其中\(\boldsymbol{y}\)表示这个线段的起点,\(\boldsymbol{x}-\boldsymbol{y}\)表示这个线段的方向,\(\alpha\)表示在这个方向上的长度的系数。
这条线段还可以表示为: \[ \{\alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y}: \alpha \in[0,1]\} \] \(\boldsymbol{x}、\boldsymbol{y}\)前的系数相加为\(1\),易于记忆。
2.2 超平面
令 \(u_1, u_2, \cdots, u_n, v \in \mathbb{R}\), 其中至少存在一个不为零的 \(u_i\) 。由所有满足线性方程 \[ u_1 x_1+u_2 x_2+\cdots+u_n x_n=v \]
的点 \(\boldsymbol{x}=\left[x_1, x_2, \cdots, x_n\right]^T\) 组成的集合称为空间 \(\mathbb{R}^n\) 的超平面。超平面可以写为: \[ \left\{\boldsymbol{x} \in \mathbb{R}^n: \boldsymbol{u}^T \boldsymbol{x}=v\right\} \]
其中\(u=\left[u_1, u_2, \cdots, u_n\right]^T\)。
注意: 超平面不一定是 \(\mathbb{R}^n\) 的子空间, 因为超平面通常不包含原点。而且超平面不一定是一个平面, 在二维空间中就是一条直线, 而三维空间中是一些普通平面。这比较好理解,因为在二维空间中可以写成\(ax+by=c\),这是一条直线;三维空间中为\(ax+by+cz=d\),表示一个平面,可以看到超平面是一个相对于\(n\)维空间下的平面。
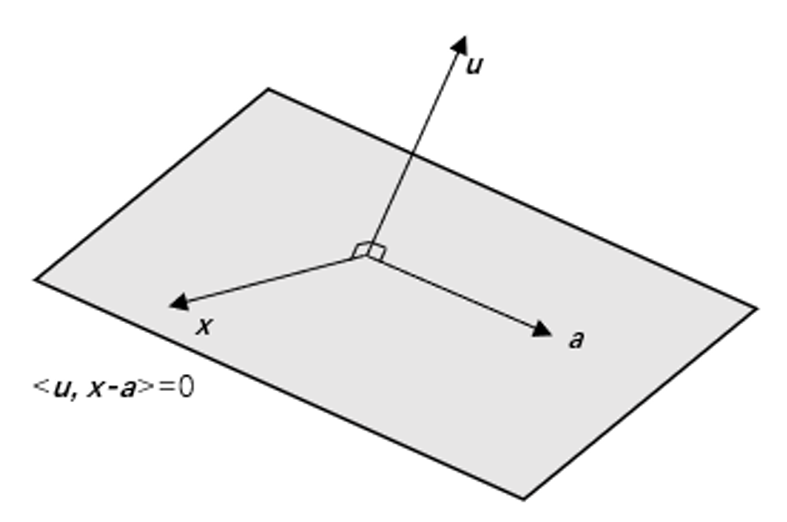
如上图,可以把超平面 \(H=\left\{\boldsymbol{x}: u_1 x_1+\cdots+u_n x_n=v\right\}\) 可以换一种形式去表述。在超平面内一点 \(\boldsymbol{a}\) 和任一点 \(\boldsymbol{x}\)。 \(\boldsymbol{u}\) 为点 \(\boldsymbol{x}\) 处的法向量,将满足 \(\boldsymbol{u^T}(\boldsymbol{x}-\boldsymbol{a})=0\) 于是有: \[ H=\left\{\boldsymbol{x} \in \mathbb{R}^n\right. : \left.\boldsymbol{u^T}(\boldsymbol{x}-\boldsymbol{a})=0\right\} \]