一个重要的反常积分

本文主要写一下反常积分$\begin{aligned} A & =\int_0^{+\infty} e^{-x^2} d x\end{aligned}$的结果及他(或变形)的计算方法，$\begin{aligned} \int_0^{+\infty} e^{-x^2} d x\end{aligned}$是一个非常重要的反常积分，在高数、概率论中有重要的应用。

方法一：二重积分

\begin{align} A&=\int_0^{+\infty} e^{-x^2} d x \\ & =\sqrt{\left(\int_0^{+\infty} e^{-x^2} d x \cdot \int_0^{+\infty} e^{-x^2} d x\right)} \\ & =\sqrt{\left(\int_0^{+\infty} e^{-x^2} d x \cdot \int_0^{+\infty} e^{-y^2} d y\right)} \\ & =\sqrt{\int_0^{+\infty} \int_0^{+\infty} e^{-\left(x^2+y^2\right)} d x d y} \end{align}

import 夹逼定理

​ 这个样子就非常非常像一个二重积分的样子了，可以利用二重积分的计算方法进行计算：

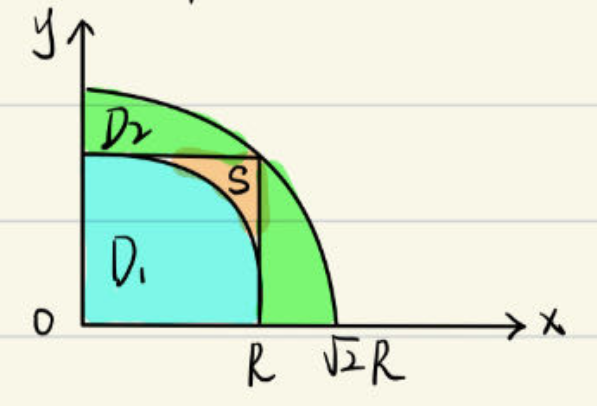
​ 如上图所示，设：

$$\begin{aligned} & D_1=\left\{(x, y) \mid x^2+y^2 \leqslant R^2, x \geqslant 0, y \geqslant 0\right\} \\ & \left.D_2=\{x, y) \mid x^2+y^2 \leqslant 2 R^2, x \geqslant 0, y \geqslant 0\right\} \\ & S=\{(x, y) \mid 0 \leqslant x \leqslant R, 0 \leqslant y \leqslant R\}\end{aligned}$$

​ 显然有：$D_1 \subset S \subset D_2$。

​ 因为：$e^{-x^2-y^2}>0$，所以：

$$\iint_{D_1} e^{-x^2-y^2} d x d y \leq \iint_S e^{-x^2-y^2} d x d y \leq \iint_{D_2} e^{-x^2-y^2} d x d y$$

​ 分别对$S、D_1、D_2$积分：

$$\left\{\begin{array}{l} \displaystyle I=\iint_S e^{-x^2-y^2} d x d y=\int_0^R e^{-x^2} d x \int_0^R e^{-y^2} d y=\left(\int_0^R e^{-x^2} d x\right)^2 \\\displaystyle I_1=\iint_{D_1} e^{-x^2-y^2} d x d y=\frac{\pi}{4}\left(1-e^{-R^2}\right) \\\displaystyle I_2=\iint_{D_2} e^{-x^2-y^2} d x d y=\frac{\pi}{4}\left(1-e^{-2 R^2}\right) \end{array}\right.$$

​ 有不等关系：$I_1<I<I_2$。

​ 当$R \rightarrow\infty$ 时, $I_1 \rightarrow \dfrac{\pi}{4}, I_2 \rightarrow \dfrac{\pi}{4}$，由夹逼定理 ：

​ 当$R \rightarrow\infty$ 时, $I\rightarrow \dfrac{\pi}{4}$。即：$\begin{aligned} \left(\int_0^{+\infty} e^{-x^2} d x\right)^2\end{aligned}=\dfrac{\pi}{4}$。

​ 所以$\begin{aligned} A & =\int_0^{+\infty} e^{-x^2} d x\end{aligned}=\dfrac{\sqrt{\pi}}{2}$

import 极坐标

​ 也可以理解成这是在极坐标下对一个半径为$+\infty$，在第一象限的扇形进行积分，设$r^2=(x^2+y^2)$，也就是：

\begin{align} A^2&= \int_0^{\frac{\pi}{2}} d\theta \int_0^{+\infty} e^{-r^2} r dr \\&= \dfrac{\pi}{2} \int_0^{+\infty} e^{-r^2} r dr \\ &= \dfrac{\pi}{4} \int_0^{+\infty} e^{-u} du \quad(u=r^2) \\&= \dfrac{\pi}{4} \end{align}

​ 所以$\begin{aligned} A & =\int_0^{+\infty} e^{-x^2} d x\end{aligned}=\dfrac{\sqrt{\pi}}{2}$

方法二：标准正态分布

设$r.v.X \sim N\left(0,1\right)$，则$X$的密度函数为：

$$p(x)=\frac{1}{\sqrt{2 \pi }} e^{-\frac{x^2}{2}},-\infty<x<+\infty$$

由密度函数的正则性：

$$\int_0^{+\infty} \varphi(x) d x=\int_0^{+\infty} \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} d x=\frac{1}{2}$$

移项得：$\begin{aligned} A & =\int_0^{+\infty} e^{-x^2} d x\end{aligned}=\dfrac{\sqrt{\pi}}{2}$

方法三：$Gamma$函数

​ $Gamma$函数是一个特殊的函数，它的定义如下：

$$\Gamma(z)=\int_0^{\infty} t^{z-1} e^{-t} \mathrm{~d} t$$

​ 在这里只介绍$Gamma$函数的几个性质：

​ 性质1.$\Gamma(z)$与阶乘的关系

$$\begin{aligned} \Gamma(z) & =\int_0^{\infty} t^{z-1} e^{-t} d t \\ & =\left.t^{z-1}\left(-e^{-t}\right)\right|_0 ^{\infty}+(z-1) \int_0^{\infty} t^{z-2} e^{-t} d t \\ & =(z-1) \int_0^{\infty} t^{(z-1)-1} e^{-t} d t \\ & =(z-1) \Gamma(z-1)\end{aligned}$$

​ 令$z=1$有：

$$\Gamma(1)=\int_0^{\infty} e^{-t} \mathrm{~d} t=-\left.e^{-t}\right|_0 ^{\infty}=1$$

​ 当$z$为整数时，有：$\Gamma(z+1)=z\Gamma(z)=z(z-1)\Gamma(z-2)=\cdots=z(z-1)(z-2)\cdots1=z!$

​ 性质2.$\Gamma(\dfrac{1}{2})=\sqrt\pi$

$$\begin{aligned} \Gamma(1/2)&= \int_0^{+\infty} x^{-1/2} e^{-x} dx \\&= \int_0^{+\infty} t^{-1} e^{-t^2} dt^2 \\ &= \int_0^{+\infty} 2 e^{-t^2} dt \\ &= 2\cdot \dfrac{\sqrt\pi}{2} \\ &= \sqrt\pi \end{aligned}$$

​ 利用$Gamma$函数计算一些变形式子的积分值：

$$\begin{aligned} & \int_0^{+\infty} {x}^3 \mathrm{e}^{-2 {x}} {dx}=\frac{1}{16} \int_0^{+\infty}(2 {x})^3 \mathrm{e}^{-2{x}} \mathrm{d}(2 {x})=\frac{1}{16} \Gamma(3+1)=\frac{3 !}{16}=\frac{3}{8} \\ & \int_0^{+\infty} {x}^4 \mathrm{e}^{-{x}^2} {dx}=\frac{1}{2} \int_0^{+\infty}\left({x}^2\right)^{\frac{3}{2}} \mathrm{e}^{-{x}^2}{dx}=\frac{1}{2} \Gamma\left(\frac{3}{2}+1\right)=\frac{1}{2} \frac{3}{2} \Gamma\left(\frac{1}{2}+1\right)=\frac{1}{2} \frac{3}{2} \frac{1}{2} \Gamma\left(\frac{1}{2}\right)=\frac{1}{2} \frac{3}{2} \frac{1}{2} \sqrt{\pi}=\frac{3}{8} \sqrt{\pi}\end{aligned}$$