一个重要的反常积分

本文主要写一下反常积分\(\begin{aligned} A & =\int_0^{+\infty} e^{-x^2} d x\end{aligned}\)的结果及他(或变形)的计算方法，\(\begin{aligned} \int_0^{+\infty} e^{-x^2} d x\end{aligned}\)是一个非常重要的反常积分，在高数、概率论中有重要的应用。

方法一：二重积分

\[ \begin{align} A&=\int_0^{+\infty} e^{-x^2} d x \\ & =\sqrt{\left(\int_0^{+\infty} e^{-x^2} d x \cdot \int_0^{+\infty} e^{-x^2} d x\right)} \\ & =\sqrt{\left(\int_0^{+\infty} e^{-x^2} d x \cdot \int_0^{+\infty} e^{-y^2} d y\right)} \\ & =\sqrt{\int_0^{+\infty} \int_0^{+\infty} e^{-\left(x^2+y^2\right)} d x d y} \end{align} \]

import 夹逼定理

​ 这个样子就非常非常像一个二重积分的样子了，可以利用二重积分的计算方法进行计算：

p1.jpg

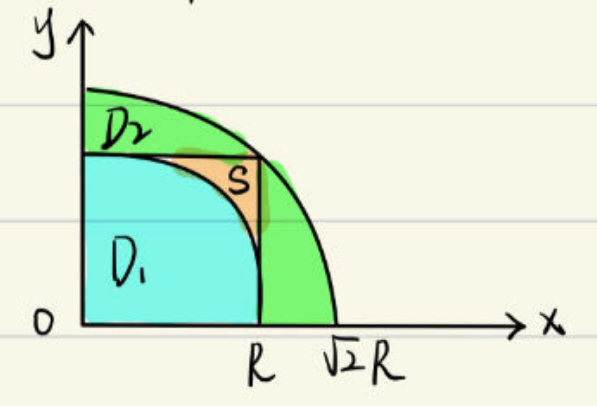
​ 如上图所示，设： \[ \begin{aligned} & D_1=\left\{(x, y) \mid x^2+y^2 \leqslant R^2, x \geqslant 0, y \geqslant 0\right\} \\ & \left.D_2=\{x, y) \mid x^2+y^2 \leqslant 2 R^2, x \geqslant 0, y \geqslant 0\right\} \\ & S=\{(x, y) \mid 0 \leqslant x \leqslant R, 0 \leqslant y \leqslant R\}\end{aligned} \] ​ 显然有：\(D_1 \subset S \subset D_2\)。

​ 因为：\(e^{-x^2-y^2}>0\)，所以： \[ \iint_{D_1} e^{-x^2-y^2} d x d y \leq \iint_S e^{-x^2-y^2} d x d y \leq \iint_{D_2} e^{-x^2-y^2} d x d y \] ​ 分别对\(S、D_1、D_2\)积分： \[ \left\{\begin{array}{l} \displaystyle I=\iint_S e^{-x^2-y^2} d x d y=\int_0^R e^{-x^2} d x \int_0^R e^{-y^2} d y=\left(\int_0^R e^{-x^2} d x\right)^2 \\\displaystyle I_1=\iint_{D_1} e^{-x^2-y^2} d x d y=\frac{\pi}{4}\left(1-e^{-R^2}\right) \\\displaystyle I_2=\iint_{D_2} e^{-x^2-y^2} d x d y=\frac{\pi}{4}\left(1-e^{-2 R^2}\right) \end{array}\right. \] ​ 有不等关系：\(I_1<I<I_2\)。

​ 当\(R \rightarrow\infty\) 时, \(I_1 \rightarrow \dfrac{\pi}{4}, I_2 \rightarrow \dfrac{\pi}{4}\)，由夹逼定理 ：

​ 当\(R \rightarrow\infty\) 时, \(I\rightarrow \dfrac{\pi}{4}\)。即：\(\begin{aligned} \left(\int_0^{+\infty} e^{-x^2} d x\right)^2\end{aligned}=\dfrac{\pi}{4}\)。

​ 所以\(\begin{aligned} A & =\int_0^{+\infty} e^{-x^2} d x\end{aligned}=\dfrac{\sqrt{\pi}}{2}\)

import 极坐标

​ 也可以理解成这是在极坐标下对一个半径为\(+\infty\)，在第一象限的扇形进行积分，设\(r^2=(x^2+y^2)\)，也就是： \[ \begin{align} A^2&= \int_0^{\frac{\pi}{2}} d\theta \int_0^{+\infty} e^{-r^2} r dr \\&= \dfrac{\pi}{2} \int_0^{+\infty} e^{-r^2} r dr \\ &= \dfrac{\pi}{4} \int_0^{+\infty} e^{-u} du \quad(u=r^2) \\&= \dfrac{\pi}{4} \end{align} \] ​ 所以\(\begin{aligned} A & =\int_0^{+\infty} e^{-x^2} d x\end{aligned}=\dfrac{\sqrt{\pi}}{2}\)

方法二：标准正态分布

设\(r.v.X \sim N\left(0,1\right)\)，则\(X\)的密度函数为： \[ p(x)=\frac{1}{\sqrt{2 \pi }} e^{-\frac{x^2}{2}},-\infty<x<+\infty \] 由密度函数的正则性： \[ \int_0^{+\infty} \varphi(x) d x=\int_0^{+\infty} \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} d x=\frac{1}{2} \] 移项得：\(\begin{aligned} A & =\int_0^{+\infty} e^{-x^2} d x\end{aligned}=\dfrac{\sqrt{\pi}}{2}\)

方法三：\(Gamma\)函数

​ \(Gamma\)函数是一个特殊的函数，它的定义如下： \[ \Gamma(z)=\int_0^{\infty} t^{z-1} e^{-t} \mathrm{~d} t \] ​ 在这里只介绍\(Gamma\)函数的几个性质：

​ 性质1.\(\Gamma(z)\)与阶乘的关系

\[ \begin{aligned} \Gamma(z) & =\int_0^{\infty} t^{z-1} e^{-t} d t \\ & =\left.t^{z-1}\left(-e^{-t}\right)\right|_0 ^{\infty}+(z-1) \int_0^{\infty} t^{z-2} e^{-t} d t \\ & =(z-1) \int_0^{\infty} t^{(z-1)-1} e^{-t} d t \\ & =(z-1) \Gamma(z-1)\end{aligned} \] ​ 令\(z=1\)有： \[ \Gamma(1)=\int_0^{\infty} e^{-t} \mathrm{~d} t=-\left.e^{-t}\right|_0 ^{\infty}=1 \] ​ 当\(z\)为整数时，有：\(\Gamma(z+1)=z\Gamma(z)=z(z-1)\Gamma(z-2)=\cdots=z(z-1)(z-2)\cdots1=z!\)

​ 性质2.\(\Gamma(\dfrac{1}{2})=\sqrt\pi\) \[ \begin{aligned} \Gamma(1/2)&= \int_0^{+\infty} x^{-1/2} e^{-x} dx \\&= \int_0^{+\infty} t^{-1} e^{-t^2} dt^2 \\ &= \int_0^{+\infty} 2 e^{-t^2} dt \\ &= 2\cdot \dfrac{\sqrt\pi}{2} \\ &= \sqrt\pi \end{aligned} \] ​ 利用\(Gamma\)函数计算一些变形式子的积分值： \[ \begin{aligned} & \int_0^{+\infty} {x}^3 \mathrm{e}^{-2 {x}} {dx}=\frac{1}{16} \int_0^{+\infty}(2 {x})^3 \mathrm{e}^{-2{x}} \mathrm{d}(2 {x})=\frac{1}{16} \Gamma(3+1)=\frac{3 !}{16}=\frac{3}{8} \\ & \int_0^{+\infty} {x}^4 \mathrm{e}^{-{x}^2} {dx}=\frac{1}{2} \int_0^{+\infty}\left({x}^2\right)^{\frac{3}{2}} \mathrm{e}^{-{x}^2}{dx}=\frac{1}{2} \Gamma\left(\frac{3}{2}+1\right)=\frac{1}{2} \frac{3}{2} \Gamma\left(\frac{1}{2}+1\right)=\frac{1}{2} \frac{3}{2} \frac{1}{2} \Gamma\left(\frac{1}{2}\right)=\frac{1}{2} \frac{3}{2} \frac{1}{2} \sqrt{\pi}=\frac{3}{8} \sqrt{\pi}\end{aligned} \]